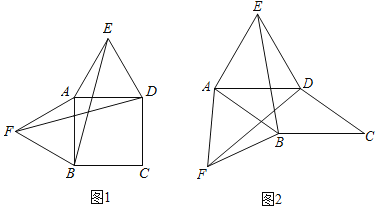
【题目】如图,以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接BE、DF.
(1)当四边形ABCD为正方形时(如图1),则线段BE与DF的数量关系是 .
(2)当四边形ABCD为平行四边形时(如图2),问(1)中的结论是否还成立?若成立,请证明;若不成立,请说明理由.
参考答案:
【答案】(1)BE=DF(或相等);(2)成立.证明见解析.
【解析】
(1)根据正方形的性质和等边三角形性质得:AB=AD,∠BAD=90°,AF=AB,AE=AD,∠BAF=∠DAE=60°,再根据全等三角形判定和性质即可.
(2)先利用平行四边形性质和等边三角形性质,再运用全等三角形判定和性质即可.
解:(1)BE=DF(或相等)如图1,
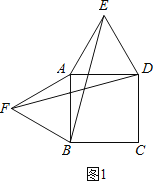
∵四边形ABCD为正方形
∴AB=AD,∠BAD=90°
∵△ABF、△ADE都是等边三角形
∴AF=AB,AE=AD,∠BAF=∠DAE=60°
∴∠BAE=∠BAD+∠DAE=150°,∠DAF=∠BAD+∠BAF=150°
∴∠BAE=∠DAF
∵AB=AF=AE=AD
∴△ABE≌△AFD(SAS)
∴BE=DF
故答案为:BE=DF或相等;
(2)成立.
证明:如图2,
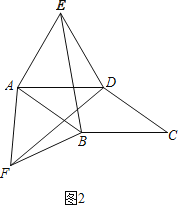
∵△AFB为等边三角形
∴AF=AB,∠FAB=60°
∵△ADE为等边三角形,
∴AD=AE,∠EAD=60°
∴∠FAB+∠BAD=∠EAD+∠BAD,
即∠FAD=∠BAE.
在△AFD和△ABE中,
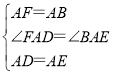 ,
,
∴△AFD≌△ABE(SAS),
∴BE=DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知⊙O的半径为1,PQ是⊙O的直径,n个相同的正三角形沿PQ排成一列,所有正三角形都关于PQ对称,其中第一个△A1B1C1的顶点A1与点P重合,第二个△A2B2C2的顶点A2是B1C1与PQ的交点……最后一个△AnBnCn的顶点Bn,Cn在圆上.



(1)如图②,当n=1时,求正三角形的边长a1.
(2)如图③,当n=2时,求正三角形的边长a2.
(3)如图①,求正三角形的边长an(用含n的代数式表示).
-
科目: 来源: 题型:
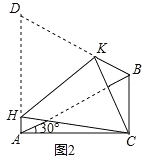
查看答案和解析>>【题目】如图1,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,E是AB的中点,连接CE并延长交AD于F.
(1)求证:△AEF≌△BEC;
(2)判断四边形BCFD是何特殊四边形,并说出理由;
(3)如图2,将四边形ACBD折叠,使D与C重合,HK为折痕,若BC=1,求AH的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如表所示
国外品牌
国内品牌
进价(万元/部)
0.44
0.2
售价(万元/部)
0.5
0.25
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可获毛利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,如果 x 与 y 都是整数,就称点(x,y)为整点.下列命题中错误的是( )
A. 存在这样的直线,既不与坐标轴平行,又不经过任何整点
B. 若 k 与 b 都是无理数,则直线 y=kx+b 不经过任何整点
C. 若直线 y=kx+b 经过无数多个整点,则 k 与 b 都是有理数
D. 存在恰好经过一个整点的直线
-
科目: 来源: 题型:
查看答案和解析>>【题目】张浩调查统计了他们家5月份每次打电话的通话时长,并将统计结果进行分组(每组含量最小值,不含最大值),将分组后的结果绘制成如图所示的频数分布直方图,则下列说法中不正确的是( )

A. 张浩家5月份打电话的总频数为80次
B. 张浩家5月份每次打电话的通话时长在5﹣10分钟的频数为15次
C. 张浩家5月份每次打电话的通话时长在10﹣15分钟的频数最多
D. 张浩家5月份每次打电话的通话时长在20﹣25分钟的频率为6%
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)探究:如图1和2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.
①如图1,若∠B、∠ADC都是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,则能证得EF=BE+DF,请写出推理过程;
②如图2,若∠B、∠D都不是直角,则当∠B与∠D满足数量关系 时,仍有EF=BE+DF;
(2)拓展:如图3,在△ABC中,∠BAC=90°,AB=AC=2
 ,点D、E均在边BC上,且∠DAE=45°.若BD=1,求DE的长.
,点D、E均在边BC上,且∠DAE=45°.若BD=1,求DE的长.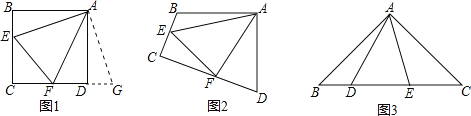
相关试题

