【题目】数形结合是重要的数学思想方法之一,数形结合具体地说就是将抽象数学语言与直观图形结合起来,使抽象思维与形象思维结合起来,通过“数”与“形”之间的对应和转变来解决数学问题。数轴是数形结合的最基础图形,是连接数与形的桥梁之一,请解决下面的问题:
(1)如图1,点B表示的数是1,则点A表示的数是 .

(2)如果点M表示数-2,将点M向右移动6个单位长度到达终点N,那么终点N表示的数是4,此时M、N两点间的距离是 .
(3)若∣x-0∣意义表示数x到原点的距离,则∣x-3∣的意义表示数x到3的距离;类似的式子∣x+3∣=4,则x= .
(4)由(3)可知,一般地,如果点A表示数为a,点B表示的数b,则A、B两点间的距离表示为 .
(5)如图2,数轴上的两个点A、B所表示的数分别是a,b,点O为原点。在a+b,a-b,∣a∣-∣b∣这三个运算结果中,是正数的有 个.
![]()
(6)利用数轴直接写出∣x-2∣+∣x+5∣的最小值= .
参考答案:
【答案】(1)-3;(2)6;(3)x=-7或x=1;(4)|a-b|;(5)1;(6)7.
【解析】
(1)直接观察数轴即可得答案;
(2)M平移了6个单位,则MN=6;
(3)∣x+3∣=4表示x到-3的距离为4,在数轴上即可发现答案;
(4)根据两数差的绝对值表示距离,即可完成解答;
(5)由数轴可以发现b<0,a>0,|b|>|a|,即可确定它们的正负;
(6)∣x-2∣+∣x+5∣最小值表示即x到2和x到-5的距离之和,通过数轴即可得出结果
解:(1)直接观察数轴即可得到,A表示的数为-3;
(2)在数轴上平移6个单位,即MN=6,故答案为:6;
(3) ∣x+3∣=4表示x到-3的距离为4,即x=-7或x=1,故答案为:x=-7或x=1;
(4)A、B两点间的距离表示为|a-b|,故答案为:|a-b|
(5)由数轴可以发现b<0,a>0,|b|>|a|,
则a+b<0,a-b>0,∣a∣-∣b∣<0,故答案为1.
(6)如图: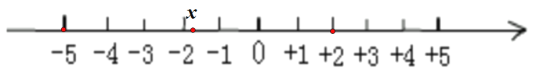
可以,发现当-5<x<2时,x到2和x到-5的距离之和均为7,不在这个范围大于7,所以∣x-2∣+∣x+5∣的最小值为7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是
 的边OB上的一点。
的边OB上的一点。过点P画OA的垂线,垂足为H;
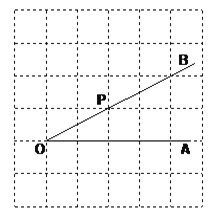
过点P画OB的垂线,交OA于点C;
线段PH的长度是点P到 的距离,_____ 是点C到直线OB的距离。因为直线外一点到直线上各点连接的所有线段中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是 。(用“<”号连接)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,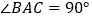 ,
,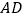 为
为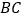 边上的中线,
边上的中线,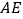 ∥
∥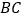 ,且
,且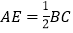 ,连接
,连接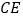 .
.(1)求证:四边形
 为菱形;
为菱形;(2)连接
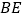 ,若
,若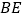 平分
平分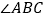 ,
,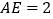 ,求
,求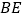 的长.
的长.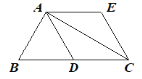
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1,第2次将点A1向右平移6个单位长度到达点A2,第3次将点A2向左移动9个单位长度到达点A3…则第6次移动到点A6时,点A6在数轴上对应的实数是_____;按照这种规律移动下去,第2017次移动到点A2017时,A2017在数轴上对应的实数是__________.
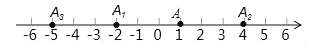
-
科目: 来源: 题型:
查看答案和解析>>【题目】南通市体育中考女生现场考试内容有三项:第一项200米跑、实心球、三级蛙跳(三选一);第二项双杠、仰卧起坐、跳绳(三选一);第三项篮球、排球、足球(三选一).小卉同学选择200米跑,双杠和篮球.小华同学第一项决定选200米跑,第二项和第三项的选择待定.
(1)请问小华同学第一项决定选200米跑的情况下有 种选择方案;
(2)用画树状图或列表的方法求小华和小卉同学在三项的选择中至少有两项方案选择一样的概率.(友情提酲:各种方案用A、B、C、…或①、②、③、…等符号来代表可简化解答过程)
-
科目: 来源: 题型:
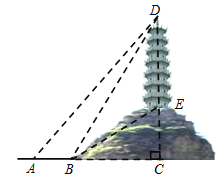
查看答案和解析>>【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)
-
科目: 来源: 题型:
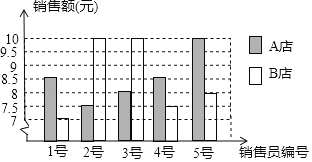
查看答案和解析>>【题目】A、B两店分另选5名销售员某月的销售额(单位:万元)进行分析,数据如下图表(不完整):
平均数
中位数
众数
A店
8.5
B店
8
10
(1)根据图a数据填充表格b所缺的数据;
(2)如果A店想让一半以上的销售员达到销售目标,你认为月销售额定为多少合适?说明理由.
相关试题

