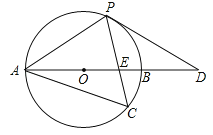
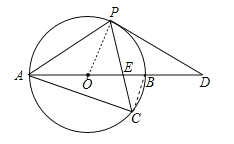
【题目】如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若点C是弧AB的中点,已知AB=4,求CECP的值.
参考答案:
【答案】(1)PD是⊙O的切线;(2)8.
【解析】
试题分析:(1)连结OP,根据圆周角定理可得∠AOP=2∠ACP=120°,然后计算出∠PAD和∠D的度数,进而可得∠OPD=90°,从而证明PD是⊙O的切线;
(2)连结BC,首先求出∠CAB=∠ABC=∠APC=45°,然后可得AC长,再证明△CAE∽△CPA,进而可得![]() ,然后可得CECP的值.
,然后可得CECP的值.
试题解析:(1)如图,PD是⊙O的切线.
证明如下:
连结OP,∵∠ACP=60°,∴∠AOP=120°,∵OA=OP,∴∠OAP=∠OPA=30°,∵PA=PD,∴∠PAO=∠D=30°,∴∠OPD=90°,∴PD是⊙O的切线.
(2)连结BC,∵AB是⊙O的直径,∴∠ACB=90°,又∵C为弧AB的中点,∴∠CAB=∠ABC=∠APC=45°,∵AB=4,AC=Absin45°=![]() .∵∠C=∠C,∠CAB=∠APC,∴△CAE∽△CPA,∴
.∵∠C=∠C,∠CAB=∠APC,∴△CAE∽△CPA,∴![]() ,∴CPCE=CA2=(
,∴CPCE=CA2=(![]() )2=8.
)2=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角

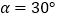 ,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角
,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角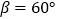 ,求树高AB(结果保留根号).
,求树高AB(结果保留根号).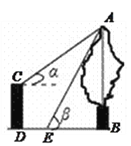
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-2x)(x2-2x+2)+1进行因式分解的过程:
解:设x2-2x=y
原式=y (y+2)+1 (第一步)
=y2+2y+1 (第二步)
=(y+1)2 (第三步)
=(x2-2x+1)2 (第四步)
请问:
(1)该同学因式分解的结果是否彻底? (填“彻底”或“不彻底”),若不彻底,则该因式分解的最终结果为 ;
(2)请你模仿上述方法,对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,部分同学随家长一同到某公园游玩,下面是购买门票时,甲同学与其爸爸的对话(如图),试根据图中的信息,解决下列问题:
(1)本次共去了几个成人,几个学生?
(2)甲同学所说的另一种购票方式,是否可以省钱?试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台.若商店保持两种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“金牛绿道行“活动需要租用
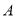 、
、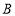 两种型号的展台,经前期市场调查发现,用
两种型号的展台,经前期市场调查发现,用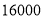 元租用的
元租用的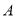 型展台的数量与用
型展台的数量与用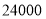 元租用的
元租用的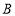 型展台的数量相同,且每个
型展台的数量相同,且每个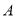 型展台的价格比每个
型展台的价格比每个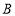 型展台的价格少
型展台的价格少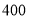 元.
元.(1)求每个
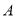 型展台、每个
型展台、每个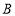 型展台的租用价格分别为多少元(列方程解应用题);
型展台的租用价格分别为多少元(列方程解应用题);(2)现预计投入资金至多
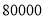 元,根据场地需求估计,
元,根据场地需求估计,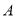 型展台必须比
型展台必须比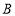 型展台多
型展台多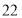 个,问
个,问 型展台最多可租用多少个.
型展台最多可租用多少个. -
科目: 来源: 题型:
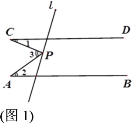
查看答案和解析>>【题目】已知直线AB∥CD,点P为直线l上一点,尝试探究并解答:
(1)如图1,若点P在两平行线之间,∠1=23°,∠2=35°,则∠3= ;
(2)探究图1中∠1,∠2与∠3之间的数量关系,并说明理由;
(3)如图2,若点P在CD的上方,探究∠1,∠2与∠3之间有怎样的数量关系,并说明理由;
(4)如图3,若∠PCD与∠PAB的平分线交于点P1,∠DCP1与∠BAP1的平分线交于点P2,∠DCP2与∠BAP2的平分线交于点P3,…,∠DCPn-1与∠BAPn-1的平分线交于点Pn,若∠PCD=α,∠PAB=β,直接写出∠APnC的度数(用含α与β的代数式表示).


相关试题

