【题目】已知直线AB∥CD,点P为直线l上一点,尝试探究并解答:
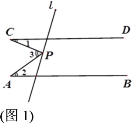
(1)如图1,若点P在两平行线之间,∠1=23°,∠2=35°,则∠3= ;
(2)探究图1中∠1,∠2与∠3之间的数量关系,并说明理由;
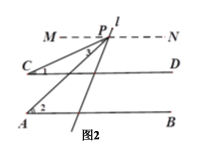
(3)如图2,若点P在CD的上方,探究∠1,∠2与∠3之间有怎样的数量关系,并说明理由;
(4)如图3,若∠PCD与∠PAB的平分线交于点P1,∠DCP1与∠BAP1的平分线交于点P2,∠DCP2与∠BAP2的平分线交于点P3,…,∠DCPn-1与∠BAPn-1的平分线交于点Pn,若∠PCD=α,∠PAB=β,直接写出∠APnC的度数(用含α与β的代数式表示).


参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() ,理由见解析;(4)
,理由见解析;(4)![]() .
.
【解析】
(1)如图1(见解析),过点P作![]() ,根据平行线的判定可得
,根据平行线的判定可得![]() ,再根据平行线的性质可得
,再根据平行线的性质可得![]() ,然后根据角的和差即可得;
,然后根据角的和差即可得;
(2)用题(1)的方法即可得;
(3)如图2(见解析),过点P作![]() ,根据平行线的判定可得
,根据平行线的判定可得![]() ,再根据平行线的性质可得
,再根据平行线的性质可得![]() ,然后根据角的和差即可得;
,然后根据角的和差即可得;
(4)先根据角平分线的定义、题(3)的结论求出![]() 的度数,再归纳类推出一般规律即可.
的度数,再归纳类推出一般规律即可.
(1)如图1,过点P作![]()
![]()
![]()
![]()
![]() ;
;

(2)结论为![]() ,理由如下:
,理由如下:
如图1,过点P作![]()
![]()
![]()
![]()
![]() ;
;
(3)结论为![]() ,理由如下:
,理由如下:
如图2,过点P作![]()
![]()
![]()
![]()
![]() ;
;
(4)由题意得:![]() 平分
平分![]() ,
,![]() 平分
平分![]() ;
;![]() 平分
平分![]() ,
,![]() 平分
平分![]() ;并且点
;并且点![]() 均在CD的上方
均在CD的上方
由角平分线的定义得:![]()
由(3)的结论得:![]()
同理可得:![]()
归纳类推得:![]() .
.
-
科目: 来源: 题型:
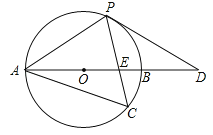
查看答案和解析>>【题目】如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若点C是弧AB的中点,已知AB=4,求CECP的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台.若商店保持两种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“金牛绿道行“活动需要租用
 、
、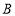 两种型号的展台,经前期市场调查发现,用
两种型号的展台,经前期市场调查发现,用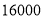 元租用的
元租用的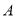 型展台的数量与用
型展台的数量与用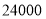 元租用的
元租用的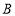 型展台的数量相同,且每个
型展台的数量相同,且每个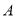 型展台的价格比每个
型展台的价格比每个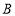 型展台的价格少
型展台的价格少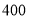 元.
元.(1)求每个
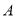 型展台、每个
型展台、每个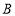 型展台的租用价格分别为多少元(列方程解应用题);
型展台的租用价格分别为多少元(列方程解应用题);(2)现预计投入资金至多
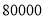 元,根据场地需求估计,
元,根据场地需求估计,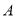 型展台必须比
型展台必须比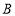 型展台多
型展台多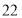 个,问
个,问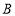 型展台最多可租用多少个.
型展台最多可租用多少个. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,广场中心菱形花坛ABCD的周长是32米,∠A=60°,则A、C两点之间的距离为( )

A. 4米 B.
 米 C. 8米 D.
米 C. 8米 D.  米
米 -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备为七年级学生开设
 共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整). 选修课
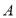
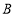
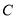
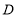
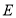
人数
40
60
100
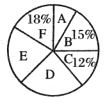
下列说法不正确的是( )
A.这次被调查的学生人数为400人B.
 对应扇形的圆心角为
对应扇形的圆心角为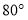
C.喜欢选修课
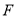 的人数为72人D.喜欢选修课
的人数为72人D.喜欢选修课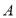 的人数最少
的人数最少 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个加工厂计划为某开发公司加工一批产品,已知甲、乙两个工厂每天分别能加工这种产品16件和24件,且单独加工这批产品甲厂比乙厂要多用20天,已知由甲厂单独做,公司需付甲厂每天费用180元;若由乙厂单独做,公司需付乙厂每天费用220元.
(1)求加工的这批产品共有多少件?
(2)若由一个加工厂单独加工完成,选用哪个加工厂费用较低?
相关试题

