【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.现随机抽取了部分学生的听写结果,绘制成如下的图表:

组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | M |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)已知该校共有900名学生,如果听写正确的字的个数少于16个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
参考答案:
【答案】(1)30;20(2)90°(3)225人
【解析】
根据两个图中B的人数和长得比例,求总人数,然后再根据比例求m,n..根据比例求角度即可.
(1)从条形图可知,B组有15人,
从扇形图可知,B组所占的百分比是15%,D组所占的百分比是30%,E组所占的百分比是20%,
15÷15%=100,
100×30%=30,
100×20%=20,
∴m=30,n=20;
故答案为30;20.
(2)“C组”所对应的圆心角的度数是25÷100×360°=90°;
故答案为90°.
(3)估计这所学校本次听写比赛不合格的
学生人数为:900×(10%+15%)
=225人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,O为坐标原点.直线y=kx+b与抛物线y=mx2﹣
 x+n同时经过A(0,3)、B(4,0).
x+n同时经过A(0,3)、B(4,0).
(1)求m,n的值.
(2)点M是二次函数图象上一点,(点M在AB下方),过M作MN⊥x轴,与AB交于点N,与x轴交于点Q.求MN的最大值.
(3)在(2)的条件下,是否存在点N,使△AOB和△NOQ相似?若存在,求出N点坐标,不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).
(1)把△ABC向上平移2个单位长度,再向右平移1个单位长度后得到△A1B1C1,请画出△A1B1C1,并写出点A1,B1,C1的坐标;
(2)求△A1B1C1的面积;
(3)点P在坐标轴上,且△A1B1P的面积是2,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一个等腰直角三角形按图示方式依次翻折,若DE=a,则①DC′平分∠BDE;②BC长为
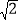 +1)a;③△BC′D是等腰三角形;④△CED的周长等于BC的长.则上述命题中正确的序号是_______.
+1)a;③△BC′D是等腰三角形;④△CED的周长等于BC的长.则上述命题中正确的序号是_______. 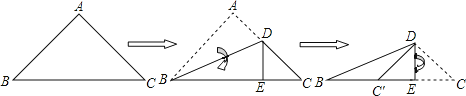
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边长为2,∠B=30°.动点P从点B出发,沿B﹣C﹣D的路线向点D运动.设△ABP的面积为y(B、P两点重合时,△ABP的面积可以看做0),点P运动的路程为x,则y与x之间函数关系的图象大致为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=3,BC=2,若AC=AD且∠ACD=60°,则对角线BD的长最大值为______________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个棱长为
 的正方体的每个面等分成
的正方体的每个面等分成 个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去
个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去 个小正方体),所得到的几何体的表面积是( )
个小正方体),所得到的几何体的表面积是( )
A. 78 B. 72 C. 54 D. 48
相关试题

