【题目】如图1,在平面直角坐标系中,O为坐标原点.直线y=kx+b与抛物线y=mx2﹣![]() x+n同时经过A(0,3)、B(4,0).
x+n同时经过A(0,3)、B(4,0).
(1)求m,n的值.
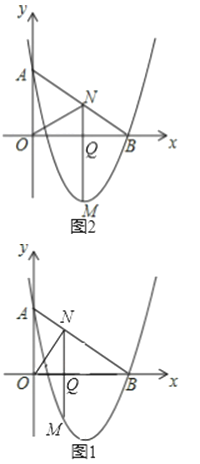
(2)点M是二次函数图象上一点,(点M在AB下方),过M作MN⊥x轴,与AB交于点N,与x轴交于点Q.求MN的最大值.
(3)在(2)的条件下,是否存在点N,使△AOB和△NOQ相似?若存在,求出N点坐标,不存在,说明理由.
参考答案:
【答案】解:(1)∵抛物线y=mx2﹣![]() x+n经过A(0,3)、B(4,0),
x+n经过A(0,3)、B(4,0),
∴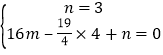 ,
,
解得![]() .
.
∴二次函数的表达式为y=x2﹣![]() x+3.
x+3.
(2)∵直线y=kx+b经过A(0,3)、B(4,0),则![]() ,
,
解得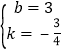 .
.
∴经过AB两点的一次函数的解析式为y=﹣![]() x+3.
x+3.
MN=﹣![]() x+3﹣(x2﹣
x+3﹣(x2﹣![]() x+3)=﹣x2+4x=﹣(x﹣2)2+4,
x+3)=﹣x2+4x=﹣(x﹣2)2+4,
∵0≤x≤4,
∴当x=2时,MN取得最大值为4.
(3)存在.
①当ON⊥AB时,(如图1)
可证:∠NOQ=∠OAB,∠OQN=∠AOB=90°,
∴△AOB∽△OQN.
∴![]()
∴OA=3,OB=4,
∴AB=5,
∵ONAB=OAOB,
∴ON=![]() ,
,
∴NQ=![]() ,OQ=
,OQ=![]() .
.
∴N(![]() ,
,![]() );
);
②当N为AB中点时,(如图2)
∠NOQ=∠B,∠AOB=∠NQO=90°,
∴△AOB∽∽△NQO.此时N(2,![]() ).
).
∴满足条件的N(![]() ,
,![]() )或N(2,
)或N(2,![]() ).
).
【解析】(1)根据抛物线y=mx2﹣![]() x+n经过A(0,3)、B(4,0),将两点坐标代入抛物线即可得出m,n的值;
x+n经过A(0,3)、B(4,0),将两点坐标代入抛物线即可得出m,n的值;
(2)根据待定系数法可求经过AB两点的一次函数的解析式,得到MN=﹣![]() x+3﹣(x2﹣
x+3﹣(x2﹣![]() x+3)=﹣x2+4x=﹣(x﹣2)2+4,从而求解;
x+3)=﹣x2+4x=﹣(x﹣2)2+4,从而求解;
(3)分两种情况讨论,①当ON⊥AB 时,②当N为AB中点时,依次求出点N的坐标即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处(如图1).
(1)如图2,设折痕与边BC交于点O,连接,OP、OA.已知△OCP与△PDA的面积比为1:4,求边AB的长;
(2)动点M在线段AP上(不与点P、A重合),动点N在线段AB的延长线上,且BN=PM,连接MN、CA,交于点F,过点M作ME⊥BP于点E.
①在图1中画出图形;
②在△OCP与△PDA的面积比为1:4不变的情况下,试问动点M、N在移动的过程中,线段EF的长度是否发生变化?请你说明理由.
-
科目: 来源: 题型:
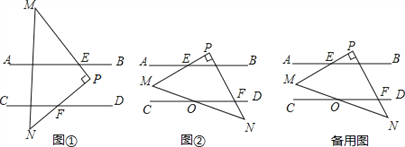
查看答案和解析>>【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F
(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为 ;
(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长是4,
 的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则
的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则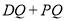 的最小值是( )
的最小值是( )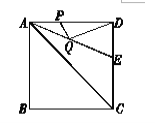
A. 2 B. 4 C.
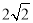 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).
(1)把△ABC向上平移2个单位长度,再向右平移1个单位长度后得到△A1B1C1,请画出△A1B1C1,并写出点A1,B1,C1的坐标;
(2)求△A1B1C1的面积;
(3)点P在坐标轴上,且△A1B1P的面积是2,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一个等腰直角三角形按图示方式依次翻折,若DE=a,则①DC′平分∠BDE;②BC长为
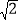 +1)a;③△BC′D是等腰三角形;④△CED的周长等于BC的长.则上述命题中正确的序号是_______.
+1)a;③△BC′D是等腰三角形;④△CED的周长等于BC的长.则上述命题中正确的序号是_______. 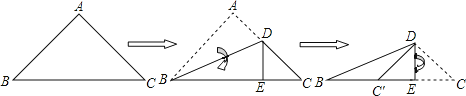
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.现随机抽取了部分学生的听写结果,绘制成如下的图表:

组别
正确字数x
人数
A
0≤x<8
10
B
8≤x<16
15
C
16≤x<24
25
D
24≤x<32
M
E
32≤x<40
n
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)已知该校共有900名学生,如果听写正确的字的个数少于16个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
相关试题

