Question

【题目】如图，己知正方形ABCD的边长为4， P是对角线BD上一点，PE⊥BC于点E， PF⊥CD于点F，连接AP， EF，给出下列结论：①PD=EC；②四边形PECF的周长为8；③△APD一定是等腰三角形；④AP=EF；⑤EF的最小值为；⑥AP⊥EF，其中正确结论的序号为（ ）

A.①②④⑤⑥B.①②④⑤C.②④⑤D.②④

Answer 1

【答案】A

【解析】

①根据正方形的对角线平分对角的性质，得△PDF是等腰直角三角形，在Rt△DPF中，DP2=DF2+PF2=EC2+EC2=2EC2，求得DP=EC．

②先证明四边形PECF为矩形，根据等腰直角三角形和矩形的性质可得其周长为2BC，则四边形PECF的周长为8；

③根据P的任意性可以判断△APD不一定是等腰三角形；

④由②可知，四边形PECF为矩形，则通过正方形的轴对称性，证明AP=EF；

⑤当AP最小时，EF最小，EF的最小值等于2；

⑥证明∠PFH+∠HPF=90°，则AP⊥EF．

①如图，延长FP交AB与G，连PC，延长AP交EF与H，

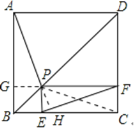
∵GF∥BC，

∴∠DPF=∠DBC，

∵四边形ABCD是正方形

∴∠DBC=45°

∴∠DPF=∠DBC=45°，

∴∠PDF=∠DPF=45°，

∴PF=EC=DF，

∴在Rt△DPF中，DP2=DF2+PF2=EC2+EC2=2EC2，

∴DP=EC．故①正确；

②∵PE⊥BC，PF⊥CD，∠BCD=90°，

∴四边形PECF为矩形，

∴四边形PECF的周长=2CE+2PE=2CE+2BE=2BC=8，故②正确；

③∵点P是正方形ABCD的对角线BD上任意一点，∠ADP=45度，

∴当∠PAD=45度或67.5度或90度时，△APD是等腰三角形，

除此之外，△APD不是等腰三角形，

故③错误．

④∵四边形PECF为矩形，

∴PC=EF，

由正方形为轴对称图形，

∴AP=PC，

∴AP=EF，

故④正确；

⑤由EF=PC=AP，

∴当AP最小时，EF最小，

则当AP⊥BD时，即AP=BD=×4=2时，EF的最小值等于2，故⑤正确；

⑥∵GF∥BC，

∴∠AGP=90°，

∴∠BAP+∠APG=90°，

∵∠APG=∠HPF，

∴∠PFH+∠HPF=90°，

∴AP⊥EF，

故⑥正确；

本题正确的有：①②④⑤⑥；

故选：A．