Question

【题目】已知⊙O的半径为r，现要在圆中画一个的菱形ABCD，

（1）当顶点D也落在圆上时，四边形ABCD的形状是___________(写出一种四边形的名称)，边长为_____________(用含r的代数式表示) ．

（2）当菱形有三个顶点落在圆上，且边长为r时，请求出作为弦的那条对角线所对的圆周角的度数．

（3）在（2）的前提下，当其中一条对角线长为3时，求该菱形的高．

Answer 1

【答案】（1）正方形， （2）60°或120°（3）或

【解析】试题分析：（1）D点在圆上时，菱形ABCD 正方形，它的对角线是圆的直径，由勾股定理可得其边长为；

（2）由题意得，D在圆心上，易求作为弦的那条对角线所对的圆周角的度数为60°或120°；

（3）分两种情况进行求解即可.

试题解析：(1)如图，

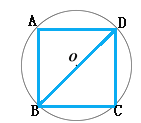
当顶点D也落在圆上时，四边形ABCD的形状是正方形.

连接BD，由勾股定理易得：BC=CD=AB=AD= ；

(2)由题意知，D在圆心上，如图，

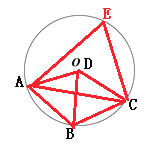
连接AC、BD，

∵四边形ABCD是菱形，且AB=BC=CD=CA=BD=r,

∴△ABD，△CBD均为等边三角形，

∴∠ABD=∠CBD=60°

∴∠ABC=120°

∵∠E+∠ABC=180°

∴∠E=60°.

即：作为弦的那条对角线所对的圆周角的度数为60°或120°；

（3）当AC=3时，可得：高；

当BD=3时，易得高

故：在（2）的前提下，当其中一条对角线长为3时，高或.