搜索
【题目】如图，在Rt△ABC中，∠BAC=90°，E、F分别是BC、AC的中点，延长BA到点D，使2AD=AB．连接DE，DF．
（1）求证：AF与DE互相平分；
（2）若BC=4，求DF的长．
参考答案：
【答案】（1）说明见解析；（2）2.
【解析】试题分析：（1）连接EF、AE，证四边形AEFD是平行四边形即可．
（2）注意应用直角三角形斜边上的中线等于斜边的一半和平行四边形的性质：平行四边形的对边相等，求得AE长即可．
试题解析：（1）连接EF，AE．
∵点E，F分别为BC，AC的中点，
∴EF∥AB，EF=
AB．
又∵AD=AB，
∴EF=AD．
又∵EF∥AD，
∴四边形AEFD是平行四边形．
∴AF与DE互相平分．
（2）在Rt△ABC中，
∵E为BC的中点，BC=4，
∴AE=BC=2．
又∵四边形AEFD是平行四边形，
∴DF=AE=2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了帮助地震灾区重建家园，某班全体师生积极捐款，捐款金额共3150元，其中5名教师人均捐款a元，则该班学生共捐款______元（用含有a的代数式表示）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】班上数学兴趣小组的同学在元旦时，互赠新年贺卡，每两个同学都相互赠送一张，小明统计出全组共互送了90张贺年卡，那么数学兴趣小组的人数是多少？设数学兴趣小组人数为x人，则可列方程为( )
A. x(x－1)＝90 B. x(x－1)＝2×90 C. x(x－1)＝90÷2 D. x(x＋1)＝90
-
科目： 来源： 题型：
查看答案和解析>>【题目】将下列各数填入相应的集合中：﹣7，0，
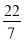，﹣22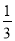
，﹣2.55555…，3.01，+9，4.020020002…，+10%， 
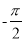．无理数集合： { …}；
负有理数集合：{ …}；
正分数集合： { …}；
非负整数集合：{ …}．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下面四个结论：
①OA=OD；②AD⊥EF；③当∠A=90°时，四边形AEDF是正方形；④AE2+DF2=AF2+DE2．
其中正确的是（ ）
A．②③④ B．②④ C．①③④ D．②③
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线．
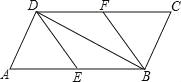
（1）求证：△ADE≌△CBF；
（2）若∠ADB是直角，则四边形BEDF是什么四边形？证明你的结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，DE平分∠ADC交BC于点E，EF⊥AD交AD于点F，若EF=3，AE=5，则AD__________．
相关试题
