【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:
①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.
其中正确的是( )

A.②③④ B.②④ C.①③④ D.②③
参考答案:
【答案】A.
【解析】
试题解析:根据已知条件不能推出OA=OD,∴①错误;
∵AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,
∴DE=DF,∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中,
![]() ,
,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∵AD平分∠BAC,
∴AD⊥EF,∴②正确;
∵∠BAC=90°,∠AED=∠AFD=90°,
∴四边形AEDF是矩形,
∵AE=AF,
∴四边形AEDF是正方形,∴③正确;
∵AE=AF,DE=DF,
∴AE2+DF2=AF2+DE2,∴④正确;
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】班上数学兴趣小组的同学在元旦时,互赠新年贺卡,每两个同学都相互赠送一张,小明统计出全组共互送了90张贺年卡,那么数学兴趣小组的人数是多少?设数学兴趣小组人数为x人,则可列方程为( )
A. x(x-1)=90 B. x(x-1)=2×90 C. x(x-1)=90÷2 D. x(x+1)=90
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各数填入相应的集合中:﹣7,0,
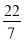 ,﹣22
,﹣22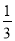 ,﹣2.55555…,3.01,+9,4.020020002…,+10%,
,﹣2.55555…,3.01,+9,4.020020002…,+10%, 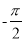 .
.无理数集合: { …};
负有理数集合:{ …};
正分数集合: { …};
非负整数集合:{ …}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使2AD=AB.连接DE,DF.
(1)求证:AF与DE互相平分;
(2)若BC=4,求DF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线.
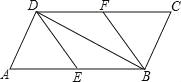
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,AE=5,则AD__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应市委政府“加快建设天蓝水碧地绿的美丽长沙”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:

请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为: ;
(2)请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民8万人,请你估计这8万人中最喜欢玉兰树的有多少人?
相关试题

