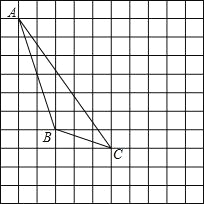
【题目】如图,每个小正方形的边长为 1 个单位,每个小方格的顶点叫格点.
(1)画出△ABC 的 AB 边上的中线 CD;
(2)画出△ABC 向右平移 4 个单位后得到的△A1B1C1;
(3)图中 AC 与 A1C1 的关系是: ;
(4)图中△ABC 的面积是 ;
(5)能使△BCE 面积为 3 的格点 E 有 个.
参考答案:
【答案】(1)见解析;(2)见解析;(3)AC 与 A1C1 平行且相等;(4)8;(5)8
【解析】(1)根据网格结构确定出AB的中点D,然后连接CD即可;
(2)根据网格结构找出点A、B、C向右平移4个单位后的对应点A1、B1、C1的位置,然后顺次连接即可;
(3)根据平移的性质解答;
(4)利用△ABC所在的矩形的面积减去四周三个直角三角形的面积和一个小长方形的面积,列式计算即可得解;
(5)首先分别在BC的两侧找到一个使其面积是3个平方单位的点E,再分别过这两点作BC的平行线,找到所有的格点即可.
(1)中线CD如图所示;
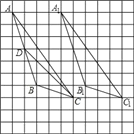
(2)△A1B1C1如图所示;
(3)AC与 A1C1平行且相等;
(4)△ABC的面积=5×7﹣![]() ×6×2﹣
×6×2﹣![]() ×3×1﹣
×3×1﹣![]() ×5×7﹣2×1=35﹣6﹣1.5﹣17.5﹣2=35﹣27=8;
×5×7﹣2×1=35﹣6﹣1.5﹣17.5﹣2=35﹣27=8;
(5)满足条件的 E 点有 8 个,如图,平行于 BC 的直线上,与网格的所有交点即为所求.
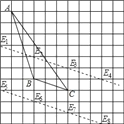
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;

(2)若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,BC=6cm.射线 AG∥BC,点 E 从点 A 出发沿射线 AG 以 2cm/s 的速度运动,当点 E 先出发 1s 后,点 F 也从点 B 出发沿射线 BC 以
 cm/s 的速度运动,分别连结 AF,CE.设点 F 运动时间为 t(s),其中 t>0.
cm/s 的速度运动,分别连结 AF,CE.设点 F 运动时间为 t(s),其中 t>0.(1)当 t 为何值时,∠BAF<∠BAC;
(2)当 t 为何值时,AE=CF;
(3)当 t 为何值时,S△ABF+S△ACE<S△ABC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级(1)班所有学生参加2016年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
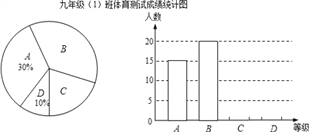
(1)、九年级(1)班参加体育测试的学生有 人;
(2)、将条形统计图补充完整.
(3)、在扇形统计图中,等级B部分所占的百分比是 ;
(4)、若该校九年级学生共有850人参加体育测试,估计达到A级和B级的学生共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=2,则△ABC的面积为( )
A.2+
B.
C.2+ 或2﹣
或2﹣ 
D.4+2 或2﹣
或2﹣ 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一个四边形纸片 ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点 B 落在 AD 边上的 B′点,AE 是折痕.
(1)试判断 B′E 与 DC 的位置关系,并说明理由;
(2)如果∠C=128°,求∠AEB 的度数.

相关试题

