【题目】已知关于x的方程k2x2﹣2(k+1)x+1=0有两个实数根.
(1)求k的取值范围;
(2)当k=1时,设所给方程的两个根分别为x1和x2 , 求 ![]() +
+ ![]() 的值.
的值.
参考答案:
【答案】
(1)解:根据题意得k2≠0且△=4(k+1)2﹣4k2≥0,
解得k≥﹣ ![]() 且k≠0;
且k≠0;
(2)解:k=1时方程化为x2﹣4x+1=0,则x1+x2=4,x1x2=1,
![]() +
+ ![]() =
= ![]() =
= ![]() =14.
=14.
【解析】(1)根据一元二次方程的定义和根的判别式的意义得到k2≠0且△=4(k+1)2﹣4k2≥0,然后解两个不等式,求出它们的公共部分即可;(2)先把k=1代入方程,再根据根与系数的关系得到x1+x2=4,x1x2=1,然后把所求的代数式变形得到 ![]() +
+ ![]() =
= ![]() ,然后利用整体思想进行计算.
,然后利用整体思想进行计算.
【考点精析】解答此题的关键在于理解求根公式的相关知识,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】跃壮五金商店准备从宁云机械厂购进甲、乙两种零件进行销售.若每个甲种零件的进价比每个乙种零件的进价少2元,且用80元购进甲种零件的数量与用100元购进乙种零件的数量相同.
(1)求每个甲种零件、每个乙种零件的进价分别为多少元?
(2)若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,该五金商店每个甲种零件的销售价格为12元,每个乙种零件的销售价格为15元,则将本次购进的甲、乙两种零件全部售出后,可使销售两种零件的总利润(利润=售价-进价)超过371元,通过计算求出跃壮五金商店本次从宁云机械厂购进甲、乙两种零件有几种方案?请你设计出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt三角形ABC中,∠ACB=90°,∠A=30° CD⊥AB于点D,那么△ACD与△BCD的面积之比为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E在边AD上,将此矩形沿CE折叠,点D落在点F处,连接BF,B、F、E三点恰好在一直线上.
(1)求证:△BEC为等腰三角形;(2)若AB=2,∠ABE=45°,求矩形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=-3x与双曲线y=
 在第四象限内的部分相交于点A(a,-6),将这条直线向
在第四象限内的部分相交于点A(a,-6),将这条直线向上平移后与该双曲线交于点M,且△AOM的面积为3.
(1)求k的值;
(2)求平移后得到的直线的函数表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数y=
 (m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x
(m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x轴于点C;M为是线段AC的中点,过点M作AC的垂线,与反比例函数的图像及y轴分别交于B、
D两点.顺次连接A、B、C、D.设点A的横坐标为n.
(1)求点B的坐标(用含有m、n的代数式表示);
(2)求证:四边形ABCD是菱形;
(3)若△ABM的面积为2,当四边形ABCD是正方形时,求直线AB的函数表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在同一直角坐标系中,反比例函数y=
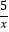 与二次函数y=﹣x2+2x+c的图象交于点A(﹣1,m).
与二次函数y=﹣x2+2x+c的图象交于点A(﹣1,m).
(1)求m、c的值;
(2)求二次函数图象的对称轴和顶点坐标.
相关试题

