【题目】如图,直线y=-3x与双曲线y=![]() 在第四象限内的部分相交于点A(a,-6),将这条直线向
在第四象限内的部分相交于点A(a,-6),将这条直线向
上平移后与该双曲线交于点M,且△AOM的面积为3.
(1)求k的值;
(2)求平移后得到的直线的函数表达式.

参考答案:
【答案】(1)k=-12; (2) y=-3x+3.
【解析】
试题(1)将点A代入直线解析式,从而得到A点坐标,再代入反比例函数解析式即可求得k;
(2)设平移后的直线交y轴于点B,连AB,根据平移可知OA//BM,又△AOM与△BOM有一条公共边OM,从而可得S△OAM=S△OAB,从而可得点B的坐标,根据直线平行时k值不变,利用待定系数法即可进行求解.
试题解析:(1)当y=-6时,x=2,∴A(2,-6),
把x=2,y=-6代入y=![]() 得:k=-12;
得:k=-12;
(2)设平移后的直线交y轴于点B,连AB.
由平移知BM∥OA,∴S△OAM=S△OAB.
又∵S△OAM=3,∴S△OAB=3,即![]() ×OB×2=3,得OB=3,即B(0,3),
×OB×2=3,得OB=3,即B(0,3),
设平移后的直线的函数表达式为y=-3x+b,把x=0,y=3代入得b=3,
∴平移后的直线的函数表达式为y=-3x+3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt三角形ABC中,∠ACB=90°,∠A=30° CD⊥AB于点D,那么△ACD与△BCD的面积之比为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E在边AD上,将此矩形沿CE折叠,点D落在点F处,连接BF,B、F、E三点恰好在一直线上.
(1)求证:△BEC为等腰三角形;(2)若AB=2,∠ABE=45°,求矩形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程k2x2﹣2(k+1)x+1=0有两个实数根.
(1)求k的取值范围;
(2)当k=1时,设所给方程的两个根分别为x1和x2 , 求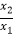 +
+  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数y=
 (m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x
(m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x轴于点C;M为是线段AC的中点,过点M作AC的垂线,与反比例函数的图像及y轴分别交于B、
D两点.顺次连接A、B、C、D.设点A的横坐标为n.
(1)求点B的坐标(用含有m、n的代数式表示);
(2)求证:四边形ABCD是菱形;
(3)若△ABM的面积为2,当四边形ABCD是正方形时,求直线AB的函数表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在同一直角坐标系中,反比例函数y=
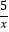 与二次函数y=﹣x2+2x+c的图象交于点A(﹣1,m).
与二次函数y=﹣x2+2x+c的图象交于点A(﹣1,m).
(1)求m、c的值;
(2)求二次函数图象的对称轴和顶点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】骑共享单车已成为人们喜爱的一种绿色出行方式.已知A、B、C三家公司的共享单车都是按骑车时间收费,标准如下:
公司
单价(元/半小时)
充值优惠
A
m
充20元送5元,即:充20元实得25元
B
m-0.2
无
C
1
充20元送20元,即:充20元实得40元
(注:使用这三家公司的共享单车,不足半小时均按半小时计费.用户的账户余额长期有效,但不可提现.)
4月初,李明注册成了A公司的用户,张红注册成了B公司的用户,并且两人在各自账户上分别充值20元.一个月下来,李明、张红两人使用单车的次数恰好相同,且每次都在半小时以内,结果到月底李明、张红的账户余额分别显示为5元、8元.
(1)求m的值;
(2)5月份,C公司在原标准的基础上又推出新优惠:每月的月初给用户送出5张免费使用券(1
次用车只能使用1张券).如果王磊每月使用单车的次数相同,且在30次以内,每次用车都不超过
半小时. 若要在这三家公司中选择一家并充值20元,仅从资费角度考虑,请你帮他作出选择,并说
明理由.
相关试题

