【题目】已知,在同一直角坐标系中,反比例函数y= ![]() 与二次函数y=﹣x2+2x+c的图象交于点A(﹣1,m).
与二次函数y=﹣x2+2x+c的图象交于点A(﹣1,m).
(1)求m、c的值;
(2)求二次函数图象的对称轴和顶点坐标.
参考答案:
【答案】
(1)解:∵点A在函数y= ![]() 的图象上,
的图象上,
∴m= ![]() =﹣5,
=﹣5,
∴点A坐标为(﹣1,﹣5),
∵点A在二次函数图象上,
∴﹣1﹣2+c=﹣5,
c=﹣2.
(2)解:∵二次函数的解析式为y=﹣x2+2x﹣2,
∴y=﹣x2+2x﹣2=﹣(x﹣1)2﹣1,
∴对称轴为直线x=1,顶点坐标为(1,﹣1).
【解析】先通过反比例函数求出A值,再把A的值代入二次函数中求出二次函数的解析式.再化简二次函数的解析式,就可得到它的对称轴和顶点坐标.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程k2x2﹣2(k+1)x+1=0有两个实数根.
(1)求k的取值范围;
(2)当k=1时,设所给方程的两个根分别为x1和x2 , 求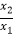 +
+  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=-3x与双曲线y=
 在第四象限内的部分相交于点A(a,-6),将这条直线向
在第四象限内的部分相交于点A(a,-6),将这条直线向上平移后与该双曲线交于点M,且△AOM的面积为3.
(1)求k的值;
(2)求平移后得到的直线的函数表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数y=
 (m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x
(m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x轴于点C;M为是线段AC的中点,过点M作AC的垂线,与反比例函数的图像及y轴分别交于B、
D两点.顺次连接A、B、C、D.设点A的横坐标为n.
(1)求点B的坐标(用含有m、n的代数式表示);
(2)求证:四边形ABCD是菱形;
(3)若△ABM的面积为2,当四边形ABCD是正方形时,求直线AB的函数表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】骑共享单车已成为人们喜爱的一种绿色出行方式.已知A、B、C三家公司的共享单车都是按骑车时间收费,标准如下:
公司
单价(元/半小时)
充值优惠
A
m
充20元送5元,即:充20元实得25元
B
m-0.2
无
C
1
充20元送20元,即:充20元实得40元
(注:使用这三家公司的共享单车,不足半小时均按半小时计费.用户的账户余额长期有效,但不可提现.)
4月初,李明注册成了A公司的用户,张红注册成了B公司的用户,并且两人在各自账户上分别充值20元.一个月下来,李明、张红两人使用单车的次数恰好相同,且每次都在半小时以内,结果到月底李明、张红的账户余额分别显示为5元、8元.
(1)求m的值;
(2)5月份,C公司在原标准的基础上又推出新优惠:每月的月初给用户送出5张免费使用券(1
次用车只能使用1张券).如果王磊每月使用单车的次数相同,且在30次以内,每次用车都不超过
半小时. 若要在这三家公司中选择一家并充值20元,仅从资费角度考虑,请你帮他作出选择,并说
明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )

A. ∠D=∠C B. BD=AC C. ∠CAD=∠DBC D. AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点A(a,3),点P在坐标轴上,若使得△AOP是等腰三角形的点P恰有6个,则满足条件的a值有( )
A. 2个 B. 3个 C. 4个 D. 5个
相关试题

