【题目】以下说法合理的是( )
A. 小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是![]()
B. 某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖
C. 某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是![]()
D. 小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是![]()
参考答案:
【答案】D
【解析】
根据各个选项中的说法可以判断是否正确,从而可以解答本题.
解:小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是![]() 是错误的,3次试验不能总结出概率,故选项A错误,
是错误的,3次试验不能总结出概率,故选项A错误,
某彩票的中奖概率是5%,那么买100张彩票可能有5张中奖,但不一定有5张中奖,故选项B错误,
某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是![]() 不正确,中靶与不中靶不是等可能事件,一般情况下,脱靶的概率大于中靶的概率,故选项C错误,
不正确,中靶与不中靶不是等可能事件,一般情况下,脱靶的概率大于中靶的概率,故选项C错误,
小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的可能性是![]() ,故选项D正确,
,故选项D正确,
故选:D.
-
科目: 来源: 题型:
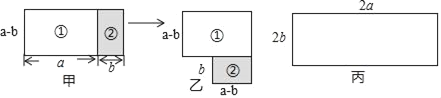
查看答案和解析>>【题目】如图所示,图甲由长方形①,长方形②组成,图甲通过移动长方形②得到图乙.
(1)S甲= ,S乙= (用含a、b的代数式分别表示);
(2)利用(1)的结果,说明a2、b2、(a+b)(a﹣b)的等量关系;
(3)现有一块如图丙尺寸的长方形纸片,请通过对它分割,再对分割的各部分移动,组成新的图形,画出图形,利用图形说明(a+b)2、(a﹣b)2、ab三者的等量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把长为22 cm的金属丝围成一个一条边长为x(cm),面积为S(cm2)的矩形框.
(1)写出用x表示S的式子;
(2)在(1)中,若S=10 cm2,请求出矩形的长和宽.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(x-3)(x-2)-p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1、x2,且满足x12+x22=3 x1x2,求实数p的值.
-
科目: 来源: 题型:
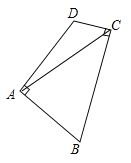
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读材料)解方程(x-1)2-5(x-1)+4=0时,我们发现:先将x-1看作一个整体,然后设x-1=y.……①,那么原方程可化为y2-5y+4=0,解得y1=1,y2=4.当y=1时,x-1=1,则x=2;当y=4时,x-1=4,则x=5,故原方程的解为x1=2,x2=5.
上述解题过程,在由原方程得到方程①的过程中,运用了“换元法”达到了解方程的目的,体现了转化的数学思想.
(解决问题)
(1)请利用以上知识解方程:(3x+5)2-4(3x+5)+3=0;
(2)在△ABC中,∠C=90°,两条直角边的长分别为a,b,斜边的长为c,且(a2+b2)(a2+b2+1)=12,求斜边c的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年5月25日,中国国际大数据产业博览会在贵阳会展中心开幕,博览会设了编号为1~6号展厅共6个,小雨一家计划利用两天时间参观其中两个展厅:第一天从6个展厅中随机选择一个,第二天从余下的5个展厅中再随机选择一个,且每个展厅被选中的机会均等.
(1)第一天,1号展厅没有被选中的概率是 ;
(2)利用列表或画树状图的方法求两天中4号展厅被选中的概率.
相关试题

