【题目】如图1，在Rt△ABC中，∠ACB = 90°．半径为1的⊙A与边AB相交于点D，与边AC相交于点E，连接DE并延长，与边BC的延长线交于点P．

（1）当∠B = 30°时，求证：△ABC∽△EPC；

（2）当∠B = 30°时，连接AP，若△AEP与△BDP相似，求CE的长；

（3）若CE = 2，BD = BC，求∠BPD的正切值．

参考答案：

【答案】（1）答案见解析；（2）；（3）

【解析】试题分析：（1）由已知条件易求∠A=60°，又因为AD=AE，所以△ADE是等边三角形，进而可得∠CEP=60°，由三角形内角和定理可求∠P=30°，继而可证明△ABC∽△EPC；

（2）根据∠B=30°，∠ACB=90°可得∠BAC=60°，从而得到△ADE是等边三角形，根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BPD=30°，然后根据等角对等边的性质可得BD=PD，再根据△AEP与△BDP相似可得PE=AE，然后根据30°角所对的直角边等于斜边的一半即可求解；

（3）设BD=BC=x，表示出AB、AC的长度，然后利用勾股定理列式求出x的值为4，过点C作CF∥DP交AB于点F，再根据平行线分线段成比例定理求出DF=2，然后求出BF的长度，再次利用平行线分线段成比例定理求出CP的长度，然后根据正切的定义解答即可．

试题解析：解：（1）∵∠ACB=90°，∠B=30°，∴∠A=60°，∵AD=AE，∴△ADE是等边三角形，∴∠ADE=∠AED=60°，∴∠PEC=∠AED=60°，∵∠ACB=∠ECP=90°，∴∠P=30°，∴△ABC∽△EPC；

（2）∵∠B=30°，∠ACB=90°，∴∠BAC=90°﹣30°=60°，∴△ADE是等边三角形，在△BDP中，∠ADE=∠B+∠BPD，即60°=30°+∠BPD，解得∠BPD=30°，∴∠B=∠BPD，∴BD=PD，∵△AEP与△BDP相似，∴AE=PE，∵⊙A的半径为1，∴PE=1，在Rt△PCE中，CE=PE=；

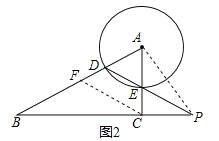
（3）设BD=BC=x，∵⊙A的半径为1，CE=2，∴AB=x+1，AC=2+1=3，∵∠ACB=90°，∴AC2+BC2=AB2，即32+x2=（x+1）2，解得x=4，过点C作CF∥DP交AB于点F，（如图2）

则，，即=，解得DF=2，∴BF=BD﹣DF=4﹣2=2，又由CF∥DP可得，即，解得CP=4，∴tan∠BPD===．

关闭