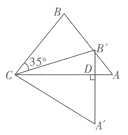
【题目】如图,把 ![]() ABC绕点C按顺时针方向旋转35
ABC绕点C按顺时针方向旋转35 ![]() ,得到△
,得到△ ![]() ,
, ![]() 交AC于点D,若
交AC于点D,若 ![]() ,则
,则 ![]() =
= ![]()
参考答案:
【答案】55
【解析】解 :∵把 △ ABC绕点C按顺时针方向旋转35 ,得到△ A ′ B ′ C ,
∴∠ACA'=35° ,
∵∠ A ′ D C = 90 ,
∴∠A'=55° ,
∵把 △ ABC绕点C按顺时针方向旋转35 ,得到△ A ′ B ′ C,
∴ △ ABC≌△ A ′ B ′ C,
∴∠A=∠A'=55° .
所以答案是 :55° 。
【考点精析】利用三角形的内角和外角和旋转的性质对题目进行判断即可得到答案,需要熟知三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,一次函数
中,一次函数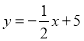 的图象
的图象 分别与
分别与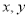 轴交于
轴交于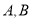 两点,正比例函数的图象
两点,正比例函数的图象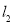 与
与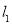 交于点
交于点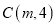
(1)求
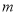 的值及
的值及 的解析式;
的解析式;(2)求
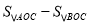 的值;
的值;(3)一次函数
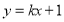 的图象为
的图象为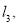 且
且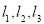 不能围成三角形,直接写出
不能围成三角形,直接写出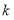 的值.
的值. -
科目: 来源: 题型:
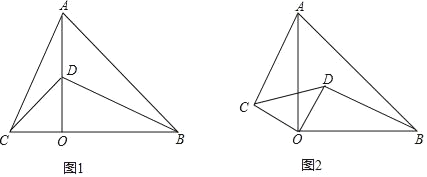
查看答案和解析>>【题目】已知,△AOB,△COD是有公共顶点的两个等腰直角三角形,∠AOB=∠COD=90°,连接AC,BD.
(1)如果△AOB,△COD的位置如图1所示,点D在AO上,请判断AC与BD的数量关系,并说明理由;
(2)如果△AOB,△COD的位置如图2所示,请判断AC与BD的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
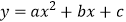 上部分点的横坐标x,纵坐标y的对应值如下表:
上部分点的横坐标x,纵坐标y的对应值如下表:x
-2
-1
0
1
2
y
0
4
6
6
4
从上表可知,下列说法中正确的是 . (填写序号)
① 抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最大值为6;
② 抛物线的对称轴是直线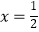 ; ④在对称轴左侧,y随x增大而增大.
; ④在对称轴左侧,y随x增大而增大. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2014cm时停下,则它停的位置是( )
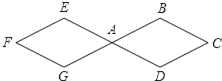
A. 点F B. 点E C. 点A D. 点C
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在
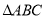 中,
中,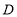 是
是 的中点,
的中点,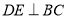 ,垂足为
,垂足为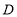 ,交
,交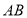 于点
于点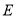 ,且
,且 .
.(1)求
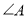 的度数;
的度数;(2)若
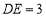 ,
,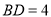 ,求
,求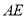 的长.
的长.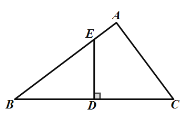
相关试题

