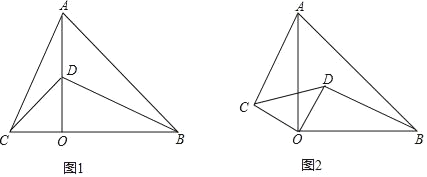
【题目】已知,△AOB,△COD是有公共顶点的两个等腰直角三角形,∠AOB=∠COD=90°,连接AC,BD.
(1)如果△AOB,△COD的位置如图1所示,点D在AO上,请判断AC与BD的数量关系,并说明理由;
(2)如果△AOB,△COD的位置如图2所示,请判断AC与BD的数量关系,并说明理由.
参考答案:
【答案】(1)结论:AC=BD.理由见解析;(2)(1)结论:AC=BD.理由见解析.
【解析】
(1)利用SAS证明△AOC≌△BOD,根据全等三角形的性质即可得;
(2)先证明∠AOC=∠BOD,继而根据SAS证明△AOC≌△BOD,即可解决问题.
(1)结论:AC=BD.
理由:∵△AOB,△COD是有公共顶点的两个等腰直角三角形,∠AOB=∠COD=90°,
∴OA=OB,OC=OD,
在△AOC和△BOD中,
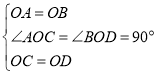 ,
,
∴△AOC≌△BOD,
∴AC=BD;
(2)结论:AC=BD.
理由:∵△AOB,△COD是有公共顶点的两个等腰直角三角形,∠AOB=∠COD=90°,
∴OA=OB,OC=OD,∠AOC=∠BOD,
在△AOC和△BOD中,
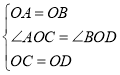 ,
,
∴△AOC≌△BOD,
∴AC=BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
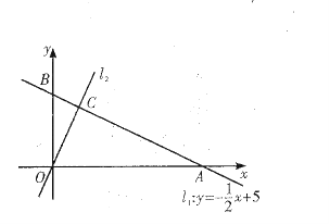
查看答案和解析>>【题目】如图,在平面直角坐标系
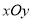 中,一次函数
中,一次函数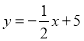 的图象
的图象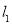 分别与
分别与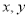 轴交于
轴交于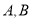 两点,正比例函数的图象
两点,正比例函数的图象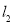 与
与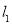 交于点
交于点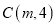
(1)求
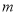 的值及
的值及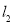 的解析式;
的解析式;(2)求
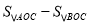 的值;
的值;(3)一次函数
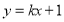 的图象为
的图象为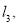 且
且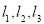 不能围成三角形,直接写出
不能围成三角形,直接写出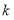 的值.
的值. -
科目: 来源: 题型:
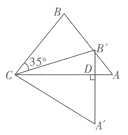
查看答案和解析>>【题目】如图,把
 ABC绕点C按顺时针方向旋转35
ABC绕点C按顺时针方向旋转35  ,得到△
,得到△ 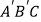 ,
, 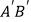 交AC于点D,若
交AC于点D,若 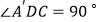 ,则
,则 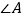 =
= 
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
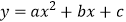 上部分点的横坐标x,纵坐标y的对应值如下表:
上部分点的横坐标x,纵坐标y的对应值如下表:x
-2
-1
0
1
2
y
0
4
6
6
4
从上表可知,下列说法中正确的是 . (填写序号)
① 抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最大值为6;
② 抛物线的对称轴是直线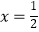 ; ④在对称轴左侧,y随x增大而增大.
; ④在对称轴左侧,y随x增大而增大. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2014cm时停下,则它停的位置是( )
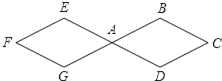
A. 点F B. 点E C. 点A D. 点C
相关试题

