【题目】如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( ) 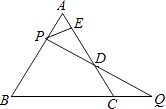
A.![]()
B.![]()
C.![]()
D.不能确定
参考答案:
【答案】B
【解析】解:过P作PM∥BC,交AC于M;
∵△ABC是等边三角形,且PM∥BC,
∴△APM是等边三角形;
又∵PE⊥AM,
∴AE=EM= ![]() AM;(等边三角形三线合一)
AM;(等边三角形三线合一)
∵PM∥CQ,
∴∠PMD=∠QCD,∠MPD=∠Q;
又∵PA=PM=CQ,
在△PMD和△QCD中
∴△PMD≌△QCD(AAS);
∴CD=DM= ![]() CM;
CM;
∴DE=DM+ME= ![]() (AM+MC)=
(AM+MC)= ![]() AC=
AC= ![]() ,故选B.
,故选B.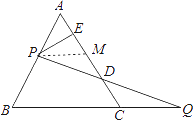
【考点精析】通过灵活运用平行线的性质和等边三角形的性质,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;等边三角形的三个角都相等并且每个角都是60°即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算: 3a(-2b)2÷6ab .
-
科目: 来源: 题型:
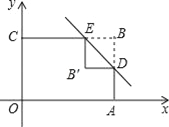
查看答案和解析>>【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(3,2).点D、E分别在AB、BC边上,BD=BE=1.沿直线DE将△BDE翻折,点B落在点B′处.则点B′的坐标为_____.
-
科目: 来源: 题型:
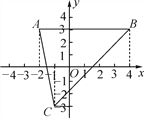
查看答案和解析>>【题目】已知点A(-2,3),B(4,3),C(-1,-3).
(1)求A,B两点之间的距离;
(2)求点C到x轴的距离;
(3)求三角形ABC的面积;
(4)观察线段AB与x轴的关系,若点D是线段AB上一点(不与A,B重合),则点D的坐标有什么特点?
-
科目: 来源: 题型:
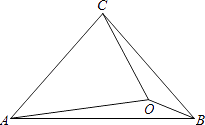
查看答案和解析>>【题目】△ABC中,∠CAB=∠CBA=50°,O为△ABC内一点,∠OAB=10°,∠OBC=20°,则∠OCA的度数为( )
A.55°
B.60°
C.70°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:(b+3a)+2(3﹣5a)﹣(6﹣2b),其中:a=﹣1,b=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式5x-12≤2(4x-3),并求出负整数解.
相关试题

