【题目】阅读下面材料:小丁在研究数学问题时遇到一个定义:对于排好顺序的三个数:x1,x2,x3,称为数列x1,x2,x3,计算![]() ,
,![]() ,
,![]() ,将这三个数的最小值称为数列x1,x2,x3的价值.例如,对于数列2,-1,3,因为
,将这三个数的最小值称为数列x1,x2,x3的价值.例如,对于数列2,-1,3,因为![]() ,
,![]() ,
,![]() ,所以数列2,-1,3的价值为
,所以数列2,-1,3的价值为![]() .
.
小丁进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的价值.如数列-1,2,3的价值为![]() ;数列3,-1,2的价值为1:…经过研究,小丁发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为
;数列3,-1,2的价值为1:…经过研究,小丁发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列4,3,-2的价值为______.
(2)将“4,3,-2”这三个数按照不同的顺序排列,可得到若干个数列,求这些数列的价值的最小值(请写出过程并作答).
(3)将3,-8,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的价值的最小值为1,则a的值为_______ (直接写出答案).
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)2或10.
;(3)2或10.
【解析】
(1)根据题中给出的材料的方法计算出相应的价值即可;(2)按照三个数不同的顺序排列出6种数列,分别求出数列的价值,确定最小价值;(3)按照三个数不同的顺序排列出6种数列,求出对应的数值,根据最小价值为1,分情况列出方程求出a值,确定符合题意进行解答.
解:(1)根据题意,
∵![]() ,
,![]() ,
,![]()
∴数列“4,3,-2”的价值为![]() ;
;
(2)①数列“4,3,-2”: ∵![]() ,
,![]() ,
,![]()
∴数列“4,3,-2”的价值为![]() ;
;
②数列“4,-2,3”: ∵![]() ,
,![]() ,
,![]()
∴数列“4,-2,3”的价值为1;
③数列“3,4,-2”: ∵![]() ,
,![]() ,
,![]()
∴数列“3,4,-2”的价值为![]() ;
;
④数列“3,-2,4”: ∵![]() ,
,![]() ,
,![]()
∴数列“3,-2,4”的价值为![]() ;
;
⑤数列“-2,4,3”: ∵![]() ,
,![]() ,
,![]()
∴数列“-2,4,3”的价值为1;
⑥数列“-2,3,4”: ∵![]() ,
,![]() ,
,![]()
∴数列“-2,3,4”的价值为![]() ;
;
∴这些数列的价值的最小值为![]() .
.
(3)①数列“3,-8,a”: ![]() ,
,![]() ,
,![]()
②数列“3,a,-8”: ![]() ,
, ![]() ,
, ![]()
③数列“-8,3,a”: ![]() ,
,![]() ,
, ![]()
④数列“-8,a,3”: ![]() ,
, ![]() ,
, ![]()
⑤数列“a,3,-8”: ![]() ,
, ![]() ,
, ![]()
⑥数列“a,-8,3”: ![]() ,
,![]() ,
,![]()
∵这些数列的价值的最小值为1,
∴当![]() 时,a=8或2,当a=8时,数列⑥中
时,a=8或2,当a=8时,数列⑥中![]() =0<1.不符合题意,a=8舍去;
=0<1.不符合题意,a=8舍去;
当![]() 时,a=-1或-5,均不符合题意,舍去;
时,a=-1或-5,均不符合题意,舍去;
当![]() 时,a=10或6,当a=6时,
时,a=10或6,当a=6时, ![]() <1.不符合题意,a=6舍去;
<1.不符合题意,a=6舍去;
∴a的值为2或10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元
 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同. 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价; 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为
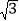 ,点E、F分别为边AD、CD上一点,将正方形分别沿BE、BF折叠,点A的对应点M恰好落在BF上,点C的对应点N恰好落在BE上,则图中阴影部分的面积为_________.
,点E、F分别为边AD、CD上一点,将正方形分别沿BE、BF折叠,点A的对应点M恰好落在BF上,点C的对应点N恰好落在BE上,则图中阴影部分的面积为_________.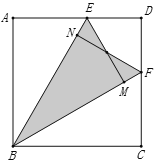
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图1中ΔABC是等边三角形,DE是中位线,F是线段BC延长线上一点,且CF=AE,连接BE,EF.
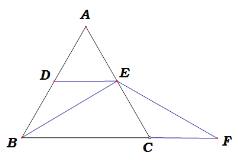
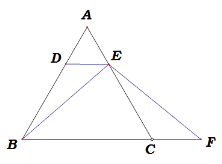
图1 图2
(1)求证:BE=EF;
(2)若将DE从中位线的位置向上平移,使点D、E分别在线段AB、AC上(点E与点A不重合),其他条件不变,如图2,则(1)题中的结论是否成立?若成立,请证明;若不成立.请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是本地区一种产品30天的销售图像,图1是产品销售量y(件)与时间t(天)的函数关系,图2是一件产品的销售利润z(元)与时间t(天)的函数关系,已知日销售利润=日销售量×每件产品的销售利润,下列结论错误的是( )。
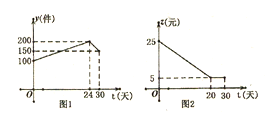
A. 第24天的销售量为200件B. 第10天销售一件产品的利润是15元
C. 第12天与第30天这两天的日销售利润相等D. 第30天的日销售利润是750元
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,
 ,求
,求 的度数. (提示:作
的度数. (提示:作 ).
). (2)如图2,
 ,当点
,当点 在线段
在线段 上运动时,
上运动时, ,求
,求 与
与 、
、 之间的数量关系,并说明理由.
之间的数量关系,并说明理由. (3)在(2)的条件下,如果点
 在射线
在射线 上运动,请你直接写出
上运动,请你直接写出 与
与 、
、 之间的数量关系.
之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、7、9、8、8
乙:7、9、6、9、9
则下列说法中错误的是( )
A.甲、乙得分的平均数都是8
B.甲得分的众数是8,乙得分的众数是9
C.甲得分的中位数是9,乙得分的中位数是6
D.甲得分的方差比乙得分的方差小
相关试题

