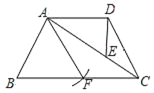
【题目】如图,已知梯形ABCD中,AD∥BC,AB=CD,点E在对角线AC上,且满足∠ADE=∠BAC.
(1)求证:CDAE=DEBC;
(2)以点A为圆心,AB长为半径画弧交边BC于点F,联结AF.求证:AF2=CECA.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据相似三角形的判定得出△ADE∽△CAB,再利用相似三角形的性质证明即可;
(2)根据相似三角形的判定得出△CDE∽△CAD,再利用相似三角形的性质证明即可.
试题解析:
证明(1)∵AD∥BC,
∴∠DAE=∠ACB,
∵∠ADE=∠BAC,
∴△ADE∽△CAB,
∴![]() ,
,
∴ABAE=DEBC,
∵AB=CD,
∴CDAE=DEBC;
(2)∵AD∥BC,AB=CD,
∴∠ADC=∠DAB,
∵∠ADE=∠BAC,
又∵∠ADC=∠ADE+∠CDE,∠DAB=∠BAC+∠CAD,
∴∠CDE=∠CAD,
∴△CDE∽△CAD,
∴![]() ,
,
∴CD2=CECA,
由题意,得AB=AF,AB=CD,
∴AF=CD,
∴AF2=CECA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠AOB和两点C、D,求作一点P,使PC=PD,且点P到∠AOB的两边的距离相等.(要求:用尺规作图,保留作图痕迹,不写作法,不要求证明)

-
科目: 来源: 题型:
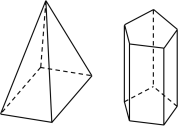
查看答案和解析>>【题目】(1)下面两个立体图形的名称是:__________,__________
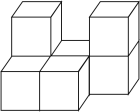
(2)一个立体图形的三视图如下图所示,这个立体图形的名称是__________

(3)画出下面立体图形的主视图.
-
科目: 来源: 题型:
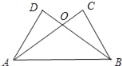
查看答案和解析>>【题目】如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
求证:△OAB是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(﹣3,1),B(0,3),C(0,1)

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1、BA1后,求四边形AB1A1B的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元
 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同. 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价; 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为
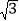 ,点E、F分别为边AD、CD上一点,将正方形分别沿BE、BF折叠,点A的对应点M恰好落在BF上,点C的对应点N恰好落在BE上,则图中阴影部分的面积为_________.
,点E、F分别为边AD、CD上一点,将正方形分别沿BE、BF折叠,点A的对应点M恰好落在BF上,点C的对应点N恰好落在BE上,则图中阴影部分的面积为_________.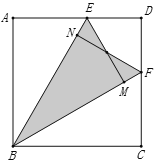
相关试题

