Question

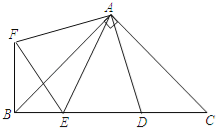
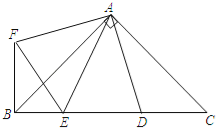
【题目】如图，在Rt△ABC中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论：①△AED≌△AEF；②AE：BE=AD：CD；③△ABC的面积等于四边形AFBD的面积；④BE2+DC2=DE2⑤BE+DC=DE其中正确的是（ ）

A. ①②④ B. ③④⑤ C. ①③⑤ D. ①③④

Answer 1

【答案】D

【解析】试题分析：①根据旋转的性质知∠CAD=∠BAF，AD=AF，∵∠BAC=90°，∠DAE=45°，∴∠CAD+∠BAE=45°．∴∠EAF=45°，∴△AED≌△AEF；故本选项正确；

②∵AB=AC，∴∠ABE=∠ACD；∴当∠BAE=∠CAD时，△ABE∽△ACD，∴=；当∠BAE≠∠CAD时，△ABE与△ACD不相似，即≠；∴此比例式不一定成立；故本选项错误；

③根据旋转的性质知△ADC≌△AFB，∴S△ABC=S△ABD+S△ABF=S四边形AFBD，即三角形ABC的面积等于四边形AFBD的面积；故本选项正确；

④∵∠FBE=45°+45°=90°，∴BE2+BF2=EF2，∵△ADC绕点A顺时针旋转90°后，得到△AFB，∴△AFB≌△ADC，∴BF=CD，又∵EF=DE，∴BE2+DC2=DE2，故本选项正确；

⑤根据①知道△AEF≌△AED，得CD=BF，DE=EF，∴BE+DC=BE+BF＞DE=EF，即BE+DC＞DE，故本选项错误；

综上所述，正确的说法是①③④；

故选D．