【题目】如图,直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y=![]() x向上平移4个单位长度后,与y轴交于点C,与双曲线y=
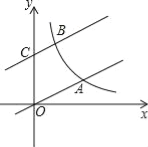
x向上平移4个单位长度后,与y轴交于点C,与双曲线y=![]() (k>0,x>0)交于点B.若OA=3BC,则k的值为 .
(k>0,x>0)交于点B.若OA=3BC,则k的值为 .
参考答案:
【答案】![]() .
.
【解析】
试题分析:分别过点A、B作AD⊥x轴,BE⊥x轴,CF⊥BE于点F,再设A(3x,![]() x),由于OA=3BC,故可得出B(x,
x),由于OA=3BC,故可得出B(x,![]() x+4),再根据反比例函数中k=xy为定值求出k的值即可.分别过点A、B作AD⊥x轴,BE⊥x轴,CF⊥BE于点F,设A(3x,
x+4),再根据反比例函数中k=xy为定值求出k的值即可.分别过点A、B作AD⊥x轴,BE⊥x轴,CF⊥BE于点F,设A(3x,![]() x),∵OA=3BC,BC∥OA,CF∥x轴,∴△BCF∽△AOD,∴CF=
x),∵OA=3BC,BC∥OA,CF∥x轴,∴△BCF∽△AOD,∴CF=![]() OD,∵点B在直线y=
OD,∵点B在直线y=![]() x+4上,∴B(x,
x+4上,∴B(x,![]() x+4),∵点A、B在双曲线y=
x+4),∵点A、B在双曲线y=![]() 上,∴3x
上,∴3x![]() x=x(
x=x(![]() x+4),解得x=1,∴k=3×1×
x+4),解得x=1,∴k=3×1×![]() ×1=
×1=![]() .故答案为
.故答案为![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某班学生做一些道具,若每小时做6个,则可以在预定时间内完成,当他们做了12个以后,掌握了其中的诀窍,每小时可做9个道具,这样他们不但提前3小时完成任务,并且多做了6个道具,则原计划用_____小时做完道具.
-
科目: 来源: 题型:
查看答案和解析>>【题目】推理说明题 已知:如图,AB∥CD,∠A=∠D,试说明AC∥DE成立的理由.下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整.
解:∵AB∥CD (已知)
∴∠A=(两直线平行,内错角相等)
又∵∠A=∠D ()
∴∠=∠(等量代换)
∴AC∥DE ()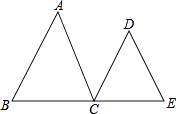
-
科目: 来源: 题型:
查看答案和解析>>【题目】图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图b的形状拼成一个正方形.
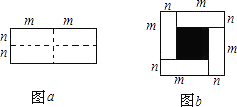
(1)你认为图b中的阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图b中阴影部分的面积. 方法1:(只列式,不化简)
方法2:(只列式,不化简)
(3)观察图b你能写出下列三个代数式之间的等式关系吗? 代数式:(m+n)2 , (m﹣n)2 , mn.
(4)根据(2)题中的等量关系,解决如下问题: 若a+b=8,ab=5.求(a﹣b)2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】化简
(1)5a+(4b﹣c)﹣3(a+3b﹣2c)
(2)3(a2﹣ab)﹣5(ab+2a2﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】若a﹣b=3,则代数式2b﹣2a+1的值是( )
A. ﹣5 B. 5 C. ﹣7 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点.
(1)在图①中以格点为顶点画一个三角形,使三角形三边长分别为2,
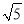 ,
,  ;
;(2)在图②中以格点为顶点画一个面积为10的正方形;
(3)观察图③中带阴影的图形,请你将它适当剪开,重新拼成一个正方形(要求:在图③中用虚线作出,并用文字说明剪拼方法).

相关试题

