【题目】如图,已知一次函数y= ![]() x+b的图象与反比例函数y=
x+b的图象与反比例函数y= ![]() (x<0)的图象交于点A(﹣1,2)和点B,点C在y轴上.
(x<0)的图象交于点A(﹣1,2)和点B,点C在y轴上.
(1)当△ABC的周长最小时,求点C的坐标;
(2)当 ![]() x+b<
x+b< ![]() 时,请直接写出x的取值范围.
时,请直接写出x的取值范围.
参考答案:
【答案】
(1)
解:作点A关于y轴的对称点A′,连接A′B交y轴于点C,此时点C即是所求,如图所示.

∵反比例函数y= ![]() (x<0)的图象过点A(﹣1,2),
(x<0)的图象过点A(﹣1,2),
∴k=﹣1×2=﹣2,
∴反比例函数解析式为y=﹣ ![]() (x<0);
(x<0);
∵一次函数y= ![]() x+b的图象过点A(﹣1,2),
x+b的图象过点A(﹣1,2),
∴2=﹣ ![]() +b,解得:b=
+b,解得:b= ![]() ,
,
∴一次函数解析式为y= ![]() x+
x+ ![]() .
.
联立一次函数解析式与反比例函数解析式成方程组: 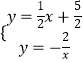 ,
,
解得: 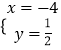 ,或
,或 ![]() ,
,
∴点A的坐标为(﹣1,2)、点B的坐标为(﹣4, ![]() ).
).
∵点A′与点A关于y轴对称,
∴点A′的坐标为(1,2),
设直线A′B的解析式为y=mx+n,
则有  ,解得:
,解得:  ,
,
∴直线A′B的解析式为y= ![]() x+
x+ ![]() .
.
令y= ![]() x+
x+ ![]() 中x=0,则y=
中x=0,则y= ![]() ,
,
∴点C的坐标为(0, ![]() )
)
(2)
解:观察函数图象,发现:
当x<﹣4或﹣1<x<0时,一次函数图象在反比例函数图象下方,
∴当 ![]() x+
x+ ![]() <﹣
<﹣ ![]() 时,x的取值范围为x<﹣4或﹣1<x<0
时,x的取值范围为x<﹣4或﹣1<x<0
【解析】(1)作点A关于y轴的对称点A′,连接A′B交y轴于点C,此时点C即是所求.由点A为一次函数与反比例函数的交点,利用待定系数法和反比例函数图象点的坐标特征即可求出一次函数与反比例函数解析式,联立两函数解析式成方程组,解方程组即可求出点A、B的坐标,再根据点A′与点A关于y轴对称,求出点A′的坐标,设出直线A′B的解析式为y=mx+n,结合点的坐标利用待定系数法即可求出直线A′B的解析式,令直线A′B解析式中x为0,求出y的值,即可得出结论;(2)根据两函数图象的上下关系结合点A、B的坐标,即可得出不等式的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+m(m>0)与x轴交于点C,与y轴交于点D,以CD为边作矩形ANCD,点A在x轴上.双曲线y=
x+m(m>0)与x轴交于点C,与y轴交于点D,以CD为边作矩形ANCD,点A在x轴上.双曲线y=  经过点B,与直线CD交于点E,则点E的坐标为( )
经过点B,与直线CD交于点E,则点E的坐标为( ) 
A.( ,﹣
,﹣  )
)
B.(4,﹣ )
)
C.( ,﹣
,﹣  )
)
D.(6,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A从点(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O、A为顶点作菱形OABC,使点B、C在第一象限内,且∠AOC=60°,点P的坐标为(0,3),设点A运动了t秒,求:
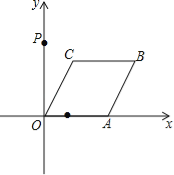
(1)点C的坐标(用含t的代数式表示);
(2)点A在运动过程中,当t为何值时,使得△OCP为等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
-
科目: 来源: 题型:
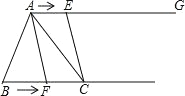
查看答案和解析>>【题目】如图,在△ABC 中,BC=6cm.射线 AG∥BC,点 E 从点 A 出发沿射线 AG 以 2cm/s 的速度运动,当点 E 先出发 1s 后,点 F 也从点 B 出发沿射线 BC 以
 cm/s 的速度运动,分别连结 AF,CE.设点 F 运动时间为 t(s),其中 t>0.
cm/s 的速度运动,分别连结 AF,CE.设点 F 运动时间为 t(s),其中 t>0.(1)当 t 为何值时,∠BAF<∠BAC;
(2)当 t 为何值时,AE=CF;
(3)当 t 为何值时,S△ABF+S△ACE<S△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O是正方形ABCD两对角线的交点. 分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转
 角(0°<
角(0°<  <360°)得到正方形
<360°)得到正方形 ,如图2.
,如图2.①在旋转过程中,当∠
 是直角时,求
是直角时,求 的度数;(注明:当直角边为斜边一半时,这条直角边所对的锐角为30度)
的度数;(注明:当直角边为斜边一半时,这条直角边所对的锐角为30度)②若正方形ABCD的边长为1,在旋转过程中,求
 长的最大值和此时
长的最大值和此时 的度数,直接写出结果不必说明理由.
的度数,直接写出结果不必说明理由.
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)求每个篮球和每个足球的售价;
(2)如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?
相关试题

