【题目】如图,直线y=﹣ ![]() x+m(m>0)与x轴交于点C,与y轴交于点D,以CD为边作矩形ANCD,点A在x轴上.双曲线y=
x+m(m>0)与x轴交于点C,与y轴交于点D,以CD为边作矩形ANCD,点A在x轴上.双曲线y= ![]() 经过点B,与直线CD交于点E,则点E的坐标为( )
经过点B,与直线CD交于点E,则点E的坐标为( ) 
A.( ![]() ,﹣
,﹣ ![]() )
)
B.(4,﹣ ![]() )
)
C.( ![]() ,﹣
,﹣ ![]() )
)
D.(6,﹣1)
参考答案:
【答案】D
【解析】解:根据题意,直线y=﹣ ![]() x+m与x轴交于C,与y轴交于D, 分别令x=0,y=0,
x+m与x轴交于C,与y轴交于D, 分别令x=0,y=0,
得y=m,x=2m,
即D(0,m),C(2m,0),
又AD⊥DC且过点D,
所以直线AD所在函数解析式为:y=2x+m,
令y=0,得x=﹣ ![]() m,
m,
即A(﹣ ![]() m,0),
m,0),
作BH⊥AC于H,
∵四边形ABCD是矩形,
∴AD=BC,∠DAO=∠BCH,
在△AOD和△CHB中
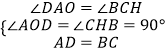
∴△AOD≌△CHB(AAS),
∴BH=OD=m,CH=OA= ![]() m,
m,
∴OH= ![]() m,
m,
∴B点的坐标为B( ![]() m,﹣m)
m,﹣m)
又B在双曲线双曲线y= ![]() (k<0)上,
(k<0)上,
∴ ![]() m(﹣m)=﹣6,
m(﹣m)=﹣6,
解得m=±2,
∵m>0,
∴m=2,
∴直线CD的解析式为y=﹣ ![]() x+2,
x+2,
解 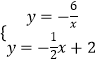 ,
,
得 ![]() 和
和 ![]() ,
,
故点E的坐标为(6,﹣1),
故选D.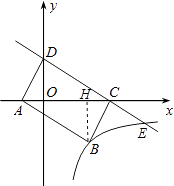
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,过点(x1 , 0),﹣3<x1<﹣2,对称轴为直线x=﹣1.给出四个结论:①abc>0;②2a+b=0;③b2>4ac;④3b+2c>0,其中正确的结论有( )

A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
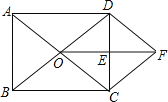
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是正方形?给出证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A从点(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O、A为顶点作菱形OABC,使点B、C在第一象限内,且∠AOC=60°,点P的坐标为(0,3),设点A运动了t秒,求:
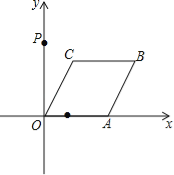
(1)点C的坐标(用含t的代数式表示);
(2)点A在运动过程中,当t为何值时,使得△OCP为等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=
 x+b的图象与反比例函数y=
x+b的图象与反比例函数y= 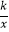 (x<0)的图象交于点A(﹣1,2)和点B,点C在y轴上.
(x<0)的图象交于点A(﹣1,2)和点B,点C在y轴上.
(1)当△ABC的周长最小时,求点C的坐标;
(2)当 x+b<
x+b< 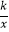 时,请直接写出x的取值范围.
时,请直接写出x的取值范围.
相关试题

