【题目】已知,正方形![]() 的边长为
的边长为![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是线段
是线段![]() 的垂直平分线与
的垂直平分线与![]() 的交点,连接
的交点,连接![]() ,并延长
,并延长![]() 交边
交边![]() 于点
于点![]() .
.
(1)如图1,若![]() 求
求![]() 的度数(用含
的度数(用含![]() 的式子表示);
的式子表示);


(2)如图2,连接![]() 当
当![]() 点运动时,探究
点运动时,探究![]() 的周长是否为定值?若是,求其值;若不是,说明理由;
的周长是否为定值?若是,求其值;若不是,说明理由;
(3)若点![]() 为
为![]() 的中点,则
的中点,则![]() 的面积为 .
的面积为 .
参考答案:
【答案】(1)![]() ;(2)是,其值为12;(3)
;(2)是,其值为12;(3)![]() .
.
【解析】
(1)证明△AGB≌△AGD,得出∠ADG=∠ABF=a,再利用三角形外角的性质即可求![]() 的度数;
的度数;
(2)将△BAF绕B点旋转90°得△BCK,证明△EBF≌△EBK得出EF=EK,即△DEF的周长=DE+DF+FE=DE+DF+EK=AD+DC即可求得;
(3)分别证明△AFG∽△CBG,△AGF∽△BGH利用相似三角形边之间关系,面积与相似比之间的关系即可求解.
解:(1)∵四边形ABCD为正方形,
∴AB=AD,∠BAC=∠DAC=45°,
又∵AG=AG,
∴△AGB≌△AGD,
∴∠ADG=∠ABF=a,
∴![]() ;
;
(2)∵四边形ABCD为正方形,
∴AB=BC,∠BAD=∠BCD=∠ADC=90°,
如下图,将△BAF绕B点旋转90°得△BCK,
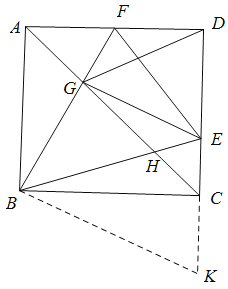
∴CK=AF,∠CBK=∠ABF=a,
∵△AGB≌△AGD,
∴BG=GD,
∵G为BE垂直平分线,
∴BG=GE,
∴BG=GD=GE,
∴∠GED=∠GDE=∠ADC-∠ADG=90°-a,
∴∠DGE=180°-2(90°-a)=2a,
∴∠BGE=∠BGD-∠DGE=2(45°-a)-2a=90°,
∴∠GBE=∠GEB=45°,
∴∠EBK=∠EBC+∠CBK=∠EBC+∠ABF=90°-∠GBE=45°,
在△EBF和△EBK中
∵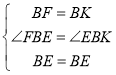
∴△EBF≌△EBK(SAS),
∴EF=EK,
∴△DEF的周长=DE+DF+FE=DE+DF+EK=AD+DC=12.
故△DEF的周长是定值,其长为12.
(3)∵F为AD的中点,
∴![]() ,
,
∵四边形ABCD为正方形,
∴AF∥BC,AD=BC=6,∠BAF=∠ABC=90°,
∴△AFG∽△CBG,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
设△AFG边AF上的高为m,△CBG边BC上的高为n,则m+n=6,![]() ,
,
解得m=2,n=4,
又∵![]() ,
,
∵∠DAC=∠GBE=45°,∠AGF=∠BGC,
∴△AGF∽△BGH,
∴![]() ,
,
∴![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①是一个新款水杯,水杯不盛水时按如图②所示的位置放置,这样可以快速晾干杯底,干净透气;将图②的主体部分抽象成图③,此时杯口与水平直线的夹角为37°,四边形ABCD可以看作矩形,测得AB=10cm,BC=8cm,过点A作AF⊥CE,交CE于点F.
(1)求∠BAF的度数;
(2)求点A到水平直线CE的距离AF的长 (参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75).

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察、思考、应用:
 .
.反之,
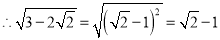
(1)仿上例,化简
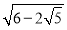 ;
;(2)若
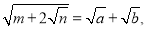 请用含
请用含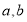 的式子分别表示
的式子分别表示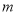 和
和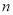 .
.(3)已知菱形
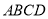 的边长为
的边长为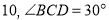 ,则菱形对角线
,则菱形对角线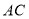 的长为 .
的长为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于
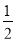 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D. 下列结论:①AD是∠BAC的平分线;②点D在AB的垂直平分线上;③∠ADC=60°;④
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D. 下列结论:①AD是∠BAC的平分线;②点D在AB的垂直平分线上;③∠ADC=60°;④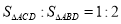 。其中正确的结论有( )
。其中正确的结论有( )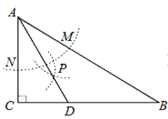
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连结CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.
(1)求证:△CDE≌△CBF;
(2)当DE=
 时,求CG的长;
时,求CG的长;(3)连结AG,在点E运动过程中,四边形CEAG能否为平行四边形?若能,求出此时DE的长;若不能,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个木制正方体的表面涂上颜色,然后将正方形分割成27个大小相同的小正方体,从这些小正方体中任意取出一个,求取出的小正方体;
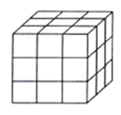
(1)只有一面涂有颜色的概率;
(2)至少有两面涂有颜色的概率;
(3)各个面都没有颜色的概率.
相关试题

