Question

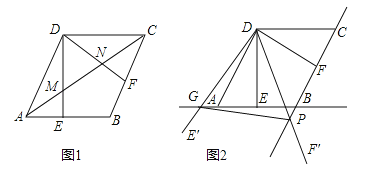
【题目】如图，在菱形ABCD中，AB=2，∠BAD=60°，过点D作DE⊥AB于点E，DF⊥BC于点F．

（1）如图1，连接AC分别交DE、DF于点M、N，求证：MN=AC；

（2）如图2，将△EDF以点D为旋转中心旋转，其两边DE′、DF′分别与直线AB、BC相交于点G、P，连接GP，当△DGP的面积等于时，求旋转角的大小并指明旋转方向．

Answer 1

【答案】（1）证明见解析；（2）将△EDF以点D为旋转中心，顺时针或逆时针旋转60°．

【解析】

试题分析：（1）连接BD，证明△ABD为等边三角形，根据等腰三角形的三线合一得到AE=EB，根据相似三角形的性质解答即可；

（2）分∠EDF顺时针旋转和逆时针旋转两种情况，根据旋转变换的性质解答即可．

试题解析：（1）证明：如图1，连接BD，交AC于O，在菱形ABCD中，∠BAD=60°，AD=AB，∴△ABD为等边三角形，∵DE⊥AB，∴AE=EB，∵AB∥DC，∴=，同理，=，∴MN=AC；

（2）解：∵AB∥DC，∠BAD=60°，∴∠ADC=120°，又∠ADE=∠CDF=30°，∴∠EDF=60°，当∠EDF顺时针旋转时，由旋转的性质可知，∠EDG=∠FDP，∠GDP=∠EDF=60°，DE=DF=，∠DEG=∠DFP=90°，在△DEG和△DFP中，∵∠GDE=∠PDF，∠DEG=∠DFP，DE=DF，∴△DEG≌△DFP，∴DG=DP，∴△DGP为等边三角形，∴△DGP的面积==，解得，DG=，则cos∠EDG=，∴∠EDG=60°，∴当顺时针旋转60°时，△DGP的面积等于；

同理可得，当逆时针旋转60°时，△DGP的面积也等于，综上所述，将△EDF以点D为旋转中心，顺时针或逆时针旋转60°时，△DGP的面积等于．