【题目】在平面直角坐标系中,抛物线y=ax2﹣5ax+4a与x轴交于A、B(A点在B点的左侧)与y轴交于点C.
(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;
(2)如图2,点P为第四象限抛物线上一点且在直线BC下方,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;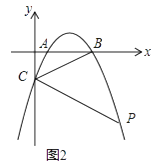
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4 ![]() a,连接KB并延长交抛物线于点Q,求PQ的长.
a,连接KB并延长交抛物线于点Q,求PQ的长.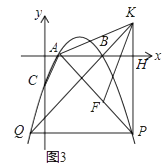
参考答案:
【答案】
(1)解:当y=0时,ax2﹣5ax+4a=0,解得x1=1,x2=4,则A(1,0),B(4,0),
∴AB=3,
∵△ABC的面积为3,
∴ ![]() 3OC=3,解得OC=2,则C(0,﹣2),
3OC=3,解得OC=2,则C(0,﹣2),
把C(0,﹣2)代入y=ax2﹣5ax+4a得4a=﹣2,解得a=﹣ ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x﹣2;
x﹣2;
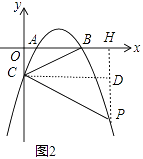
(2)解:过点P作PH⊥x轴于H,作CD⊥PH于点H,如图2,设P(x,ax2﹣5ax+4a),则PD=4a﹣(ax2﹣5ax+4a)=﹣ax2+5ax,
∵AB∥CD,
∴∠ABC=∠BCD,
∵∠BCP=2∠ABC,
∴∠PCD=∠ABC,
∴Rt△PCD∽Rt△CBO,
∴PD:OC=CD:OB,
即(﹣ax2+5ax):(﹣4a)=x:4,解得x1=0,x2=6,
∴点P的横坐标为6;
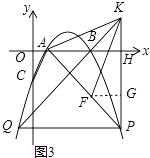
(3)解:过点F作FG⊥PK于点G,如图3,
∵AK=FK,
∴∠KAF=∠KFA,
而∠KAF=∠KAH+∠PAH,∠KFA=∠PKF+∠KPF,
∵∠KAH=∠FKP,
∴∠HAP=∠KPA,
∴HA=HP,
∴△AHP为等腰直角三角形,
∵P(6,10a),
∴﹣10a=6﹣1,解得a=﹣ ![]() ,
,
在Rt△PFG中,∵PF=﹣4 ![]() a=2
a=2 ![]() ,∠FPG=45°,
,∠FPG=45°,
∴FG=PG= ![]() PF=2,
PF=2,
在△AKH和△KFG中
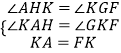 ,
,
∴△AKH≌△KFG,
∴KH=FG=2,
∴K(6,2),
设直线KB的解析式为y=mx+n,
把K(6,2),B(4,0)代入得 ![]() ,
,
解得 ![]() ,
,
∴直线KB的解析式为y=x﹣4,
当a=﹣ ![]() 时,抛物线的解析式为y=﹣
时,抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x﹣2,
x﹣2,
解方程组 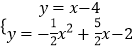 ,
,
解得 ![]() 或
或 ![]() ,
,
∴Q(﹣1,﹣5),
而P(6,﹣5),
∴PQ∥x 轴,
∴QP=7.
【解析】(1)观察函数解析式的特点,求出此函数图像与x轴的交点A、B的坐标,注意:A点在B点的左侧,用待定系数法就可以求出此函数解析式。
(2)根据已知添加辅助线,过点P作PH⊥x轴于H,作CD⊥PH于点H,易证得Rt△PCD∽Rt△CBO,得出对应边成比例,抓住点P在第四象限,设点P的坐标,建立方程,求解即可求出点P的坐标。
(3)过点F作FG⊥PK于点G,先证∠HAP=∠KPA得到HA=HP,根据点P的坐标即可求出a的值,就可以证得△AHP为等腰直角三角形,再证明△AKH≌△KFG,得出KH=FG,即可得到点K的坐标,再求出直线KB的解析式,两函数图像交于点Q,因此由两函数解析式联立方程,求解即可求得Q点坐标,即可求得QP的值。
【考点精析】本题主要考查了确定一次函数的表达式和相似三角形的判定与性质的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF,连接AF,BF,DE,CE,分别交于H,G.求证:
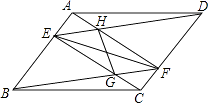
(1)EF与GH互相平分;
(2)在不添加任何辅助线和字母的条件下,请直接写出图中所有的全等的三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】六一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
(1)求A、B两种品牌服装每套进价分别为多少元?
(2)该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校七年级800名学生的跳绳情况(60秒跳绳的次数),随机对该年级50名学生进行了调查,根据收集的数据绘制了如图所示的频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的次数x为:
 ,则以下说法正确的是( )
,则以下说法正确的是( )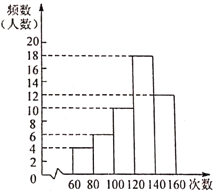
A. 跳绳次数最多的是160次
B. 大多数学生跳绳次数在140-160范围内
C. 跳绳次数不少于100次的占80%
D. 由样本可以估计全年级800人中跳绳次数在60-80次的大约有70人
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作⊙O切线EF交BA的延长线于F.
(1)如图1,求证:EF∥AC;
(2)如图2,OP⊥AO交BE于点P,交FE的延长线于点M.求证:△PME是等腰三角形;
(3)如图3,在(2)的条件下:CG⊥AB于H点,交⊙O于G点,交AC于Q点,如图2,若sinF= ,EQ=5,求PM的值.
,EQ=5,求PM的值.
-
科目: 来源: 题型:
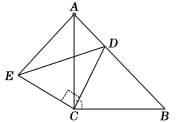
查看答案和解析>>【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
求证:(1)△ACE≌△BCD;(2)
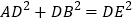 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
相关试题

