【题目】如图,在平面直角坐标系中,直线AB与坐标轴分别交于A、B两点,已知点A的坐标为(0,8),点B的坐标为(8,0),OC、AD均是△OAB的中线,OC、AD相交于点F,OE⊥AD于G交AB于E.
(1)点C的坐标为__________;
(2)求证:△AFO≌△OEB;
(3)求证:∠ADO=∠EDB

参考答案:
【答案】(1)点C的坐标为(4,4);(2)证明见解析;(3)证明见解析.
【解析】试题分析:(1)先求出OA,OB进而求出OC,再用待定系数法求出直线AB的解析式,设出点C的坐标,即可得出结论;
(2)先判断出∠AOC=∠OBA,再利用互余判断出∠OAD=∠EOD,即可得出结论;
(3)先确定出OE的解析式,进而求出点E的坐标,即可求出直线DE的解析式,进而判断出OA=OM,即可得出结论.
试题解析:(1)A(0,8),B(0,8),
∴AB=8![]() ,OA=OB,
,OA=OB,
∴△AOB是等腰直角三角形,
∵OC是△AOB的中线,
∴OC=![]() AB=4
AB=4![]() ,
,
设直线AB的解析式为y=kx+b,
∵B(8,0),A(0,8),
∴![]() ,
,
∴![]() ,
,
∴直线AB的解析式为y=-x+8,
设点C(m,-m+8),OC=![]() ,
,
∴m=4
∴C(4,4);
(2)由(1)知,OC是等腰直角三角形的斜边的中线,
∴∠AOC=45°=∠OBA,
∵OE⊥AD,
∴∠EOD+∠ODA=90°,
∵∠ADO+∠OAD=90°,
∴∠OAD=∠EOD,
在△AOF和△OBE中,
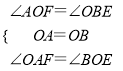 ,
,
∴△AOF≌△OBE;
(3)如图,
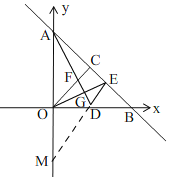
∵AD是△AOB的中线,
∴OD=BD,
∵B(8,0),
∴D(4,0),
∴直线AD的解析式为y=-2x+8,
∵OE⊥AD,
∴直线OE的解析式为y=![]() x,
x,
∵点E在直线AB上,
∴ ,解得,
,解得, 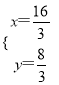 ,
,
∴E(![]() ,
, ![]() ),
),
∵D(4,0),
∴直线DE的解析式为y=2x-8,
∴OM=8,
∴OA=OM,
∵OB⊥OA,
∴AD=MD,
∴∠ADO=∠MDO.
∵∠EDB=∠MDO,
∴∠ADO=∠EDB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年某区为绿化行车道,计划购买甲、乙两种树苗共计n棵.设购买甲种树苗x棵,有关甲、乙两种树苗的信息如图所示.
(1)当n=500时,
①根据信息填表(用含x的式子表示);
树苗类型
甲种树苗
乙种树苗
购买树苗数量(单位:棵)
x
购买树苗的总费用(单位:元)
②如果购买甲、乙两种树苗共用去25 600元,那么甲、乙两种树苗各购买了多少棵?
(2)要使这批树苗的成活率不低于92%,且使购买这两种树苗的总费用为26 000元,求n的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】绿豆在相同条件下的发芽试验,结果如下表所示:
每批
粒数n
100
300
400
600
1000
2000
3000
发芽的
粒数m
96
282
382
570
948
1912
2850
发芽的
频率

0.960
0.940
0.955
0.950
0.948
0.956
0.950
则绿豆发芽的概率估计值是( )
A. 0.96 B. 0.95 C. 0.94 D. 0.90
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列试验中,概率最大的是( )
A. 抛掷一枚质地均匀的硬币,出现正面的概率
B. 抛掷一枚质地均匀的正方体骰子(六个面分别刻有数字1到6),掷出的点数为奇数的概率
C. 在一副洗匀的扑克(背面朝上)中任取一张,恰好为方块的概率
D. 三张同样的纸片,分别写有数字2、3、4,洗匀后背面向上,任取一张恰好为偶数的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】某镇水库的可用水量为12000万m3,假设年降水量不变,能维持该镇16万人20年的用水量.为实施城镇化建设,新迁入了4万人后,水库只能够维持居民15年的用水量.
(1)问:年降水量为多少万m3?每人年平均用水量多少m3?
(2)政府号召节约用水,希望将水库的使用年限提高到25年.则该镇居民人均每年需节约多少m3水才能实现目标?
(3)某企业投入1000万元设备,每天能淡化5000m3海水,淡化率为70%.每淡化1m3海水所需的费用为1.5元,政府补贴0.3元.企业将淡化水以3.2元/m3的价格出售,每年还需各项支出40万元.按每年实际生产300天计算,该企业至少几年后能收回成本(结果精确到个位)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
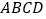 是矩形,点
是矩形,点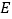 在线段
在线段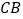 的延长线上,连接
的延长线上,连接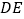 交
交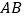 于点
于点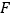 ,
,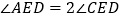 ,点
,点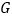 是
是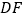 的中点.
的中点.(
 )求证:
)求证: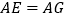 .
.(
 )若
)若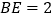 ,
,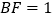 ,
,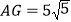 ,点
,点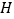 是
是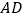 的中点,求
的中点,求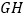 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条直线上依次有
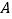 、
、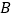 、
、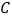 三个港口,甲、乙两船同时分别从
三个港口,甲、乙两船同时分别从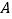 、
、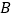 港口出发,沿直线匀速驶向
港口出发,沿直线匀速驶向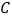 港,最终达到
港,最终达到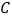 港.设甲、乙两船行驶
港.设甲、乙两船行驶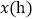 后,与
后,与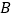 港的距离分别为
港的距离分别为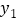 、
、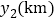 ,
,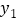 、
、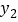 与
与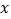 的函数关系如图所示.
的函数关系如图所示. (
 )填空:
)填空: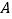 、
、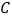 两港口间的距离为__________
两港口间的距离为__________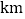 ,
,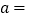 __________.
__________.(
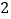 )求图中点
)求图中点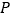 的坐标.
的坐标.(
 )若两船的距离不超过
)若两船的距离不超过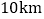 时能够相互望见,求甲、乙两船可以相互望见时
时能够相互望见,求甲、乙两船可以相互望见时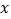 的取值范围.
的取值范围.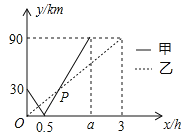
相关试题

