【题目】如图是某地下商业街的入口,数学课外兴趣小组的同学打算运用所学的知识测量侧面支架的最高点E到地面的距离EF.经测量,支架的立柱BC与地面垂直,即∠BCA=90°,且BC=1.5m,点F、A、C在同一条水平线上,斜杆AB与水平线AC的夹角∠BAC=30°,支撑杆DE⊥AB于点D,该支架的边BE与AB的夹角∠EBD=60°,又测得AD=1m.请你求出该支架的边BE及顶端E到地面的距离EF的长度. 
参考答案:
【答案】解:过B作BH⊥EF于点H, ∴四边形BCFH为矩形,BC=HF=1.5m,∠HBA=∠BAC=30°,
在Rt△ABC中,
∵∠BAC=30°,BC=1.5m,
∴AB=3m,
∵AD=1m,
∴BD=2m,
在Rt△EDB中,
∵∠EBD=60°,
∴∠BED=90°﹣60°=30°,
∴EB=2BD=2×2=4m,
又∵∠HBA=∠BAC=30°,
∴∠EBH=∠EBD﹣∠HBD=30°,
∴EH= ![]() EB=2m,
EB=2m,
∴EF=EH+HF=2+1.5=3.5(m).
答:该支架的边BE为4m,顶端E到地面的距离EF的长度为3.5m.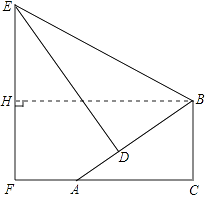
【解析】过B作BH⊥EF于点H,在Rt△ABC中,根据∠BAC=30°,BC=1.5,可求得AB的长度,又AD=1m,可求得BD的长度,在Rt△EBD中解直角三角形求得EB的长度,然后根据BH⊥EF,求得∠EBH=30°,继而可求得EH的长度,易得EF=EH+HF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E为BC边上的一点,连结AE、BD且AE=AB.
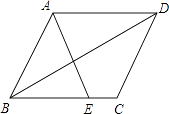
(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】实践操作

如图,△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
(1)作∠BAC的平分线,交BC于点O;
(2)以O为圆心,OC为半径作圆.
(3)在你所作的图中,AB与⊙O的位置关系是;(直接写出答案)
(4)若AC=5,BC=12,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少2元,发现原来买这种水果80千克的钱,现在可买88千克.
(1)现在实际购进这种水果每千克多少元?
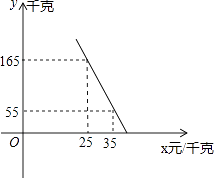
(2)王阿姨准备购进这种水果销售,若这种水果的销售量y(千克)与销售单价x(元/千克)满足如图所示的一次函数关系. ①求y与x之间的函数关系式;
②请你帮王阿姨拿个主意,将这种水果的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入﹣进货金额) -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料
如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=90°,且点D在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD.
解决问题
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出 的值(用含α的式子表示出来)
的值(用含α的式子表示出来) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,若二次函数y=
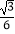 x2+bx+c的图象与x轴交于A(﹣2,0),B(3,0)两点,点A关于正比例函数y=
x2+bx+c的图象与x轴交于A(﹣2,0),B(3,0)两点,点A关于正比例函数y= 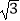 x的图象的对称点为C.
x的图象的对称点为C.
(1)求b、c的值;
(2)证明:点C在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数y=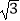 x的图象于点D,连结AC,交正比例函数y=
x的图象于点D,连结AC,交正比例函数y= 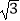 x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.
x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市在招商引资期间,把已倒闭的机床厂租给外地某投资商,该投资商为减小固定资产投资,将原有的正方形场地改建成800平方米的长方形场地,且其长、宽的比为5:2.
(1)求改建后的长方形场地的长和宽为多少米?
(2)如果把原来面积为900平方米的正方形场地的金属栅栏围墙全部利用,来作为新场地的长方形围墙,栅栏围墙是否够用?为什么?
相关试题

