【题目】某市在招商引资期间,把已倒闭的机床厂租给外地某投资商,该投资商为减小固定资产投资,将原有的正方形场地改建成800平方米的长方形场地,且其长、宽的比为5:2.
(1)求改建后的长方形场地的长和宽为多少米?
(2)如果把原来面积为900平方米的正方形场地的金属栅栏围墙全部利用,来作为新场地的长方形围墙,栅栏围墙是否够用?为什么?
参考答案:
【答案】(1)长和宽分别为20![]() 米、8
米、8![]() 米;(2)这些金属栅栏不够用.
米;(2)这些金属栅栏不够用.
【解析】
(1)设长方形围场长为5x米,则其宽为2x米,根据长方形面积列出方程求出x的值,进而可知长方形长与宽;
(2)由(1)中长方形的长与宽可知长方形周长,同理可得正方形的周长,比较大小可知是否够用.
(1)设长方形围场长为5x米,则其宽为2x米,根据题意,
得:5x2x=800,
解得:x=4![]() 或x=﹣4
或x=﹣4![]() (舍),
(舍),
∴长=4![]() ×5=20
×5=20![]() ,宽=4
,宽=4![]() ×2=8
×2=8![]() ,
,
答:改建后的长方形场地的长和宽分别为20![]() 米、8
米、8![]() 米;
米;
(2)设正方形边长为y,则y2=900,
解得:y=30或y=﹣30(舍),
原正方形周长为120米,
新长方形的周长为(20![]() +8
+8![]() )×2=56
)×2=56![]() ,
,
∵120<56![]() ,
,
∴栅栏不够用,
答:这些金属栅栏不够用.
-
科目: 来源: 题型:
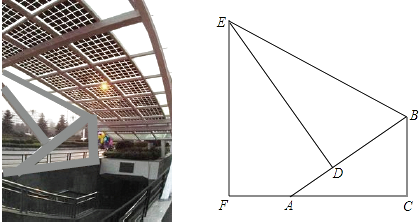
查看答案和解析>>【题目】如图是某地下商业街的入口,数学课外兴趣小组的同学打算运用所学的知识测量侧面支架的最高点E到地面的距离EF.经测量,支架的立柱BC与地面垂直,即∠BCA=90°,且BC=1.5m,点F、A、C在同一条水平线上,斜杆AB与水平线AC的夹角∠BAC=30°,支撑杆DE⊥AB于点D,该支架的边BE与AB的夹角∠EBD=60°,又测得AD=1m.请你求出该支架的边BE及顶端E到地面的距离EF的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料
如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=90°,且点D在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD.
解决问题
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出 的值(用含α的式子表示出来)
的值(用含α的式子表示出来) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,若二次函数y=
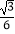 x2+bx+c的图象与x轴交于A(﹣2,0),B(3,0)两点,点A关于正比例函数y=
x2+bx+c的图象与x轴交于A(﹣2,0),B(3,0)两点,点A关于正比例函数y= 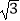 x的图象的对称点为C.
x的图象的对称点为C.
(1)求b、c的值;
(2)证明:点C在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数y=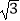 x的图象于点D,连结AC,交正比例函数y=
x的图象于点D,连结AC,交正比例函数y= 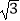 x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.
x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正八边形ABCDEFGH中,四边形BCFG的面积为20cm2 , 则正八边形的面积为cm2 .
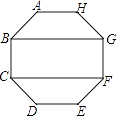
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算:|﹣2|﹣ +(﹣2013)0;
+(﹣2013)0;
(2)计算:(1+ )÷
)÷ 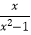 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读材料)
∵
 <
< <
< ,即2<
,即2< <3,
<3,∴1<
 <2.
<2.∴
 ﹣1的整数部分为1.
﹣1的整数部分为1.∴
 ﹣1的小数部分为
﹣1的小数部分为 ﹣2
﹣2(解决问题)9的小数部分是 ;
我们还可以用以下方法求一个无理数的近似值.
阅读理解:求
 的近似值.
的近似值.解:设
 =10+x,其中0<x<1,则107=(10+x)2,即107=100+20x+x2.
=10+x,其中0<x<1,则107=(10+x)2,即107=100+20x+x2.因为0<x<1,所以0<x2<1,所以107≈100+20x,解之得x≈0.35,即
 的近似值为10.35.
的近似值为10.35.理解应用:利用上面的方法求
 的近似值(结果精确到0.01).
的近似值(结果精确到0.01).
相关试题

