【题目】如图,两个形状、大小完全相同的含有30。角的直角三角板如图1放置,PA、PB与直线MN重合,且三角板PAC和三角板PBD均可以绕点P逆时针旋转.
(1)如图1.则∠DPC为多少度?
(2)如图2,若三角板PAC的边PA从PN处开始绕点P逆时针旋转的角度为α,PF平分∠APD,PE平分∠CPD,求∠EPF的度数;
(3)如图3,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3。/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2。/秒,在两个三角板旋转过程中,当PC转到与PM重合时,两个三角板都停止转动.设两个三角板旋转时间为t秒,请问 ![]() 是定值吗?若是定值,请求出这个定值;若不是定值,请说明理由。
是定值吗?若是定值,请求出这个定值;若不是定值,请说明理由。
参考答案:
【答案】
(1)解:∵∠DPC=180°-∠CPA-∠DPB,∠CPA=60°,∠DPB=30°,
∴∠DPC=180゜-30゜-60゜=90゜
(2)
(3)解: ![]() 是定值,理由如下:
是定值,理由如下:
设运动时间为t秒 ![]() ,则∠NPA=3t,∠MPB=2t,
,则∠NPA=3t,∠MPB=2t,
∴∠BPN=1800-2t,
∠CPD=3600-∠DPB-∠BPN-∠NPA-∠CPA=900-t,
∴ ![]()
【解析】(1)利用含有30゜、60゜的三角板得出∠DPC=180°-∠CPA-∠DPB,代入计算即可;
(2)根据角平分线的定义得出∠DPF=![]() ∠APD,∠DPE=
∠APD,∠DPE=![]() ∠CPD ,根据角的和差得出APD=180°30°α=150°α ,∠CPD=180°30°60°α=90°α ,从而得出∠DPF及,∠DPE的度数,最后根据EPF=∠DPF∠DPE算出结果;
∠CPD ,根据角的和差得出APD=180°30°α=150°α ,∠CPD=180°30°60°α=90°α ,从而得出∠DPF及,∠DPE的度数,最后根据EPF=∠DPF∠DPE算出结果;
(3)首先得出![]() 是一个定值, 设运动时间为t秒,则∠BPM=2t,∠NPA=3t ,∠BPN=1800-2t ,∠CPD=3600-∠DPB-∠BPN-∠NPA-∠CPA=900-t ,即可得出答案.
是一个定值, 设运动时间为t秒,则∠BPM=2t,∠NPA=3t ,∠BPN=1800-2t ,∠CPD=3600-∠DPB-∠BPN-∠NPA-∠CPA=900-t ,即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AB的中垂线DE交AB于E,交BC于D,若AB=10,AC=6,则△ACD的周长为( )

A.16
B.14
C.20
D.18 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=4
 ,CD=2
,CD=2  ,点P在四边形ABCD的边上,若点P到BD的距离为3,则点P的个数为( )
,点P在四边形ABCD的边上,若点P到BD的距离为3,则点P的个数为( ) 
A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知4×8 m×16 m=2 9,则m的值是( )
A. 1 B. 4 C. 3 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一列按一定顺序和规律排列的数:
第一个数是
 ;
;第二个数是
 ;
;第三个数是
 ;
;…
对任何正整数n,第n个数与第(n+1)个数的和等于
 .
.(1)经过探究,我们发现:
 ,
,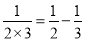 ,
, ;
;设这列数的第5个数为a,那么
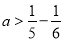 ,
, ,
, ,哪个正确?
,哪个正确?请你直接写出正确的结论;
(2)请你观察第1个数、第2个数、第3个数,猜想这列数的第n个数(即用正整数n表示第n数),并且证明你的猜想满足“第n个数与第(n+1)个数的和等于
 ”;
”;(3)设M表示
 ,
, ,
, ,…,
,…, ,这2016个数的和,即
,这2016个数的和,即 ,求证:
,求证: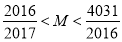 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,若有下列四个条件:①AB//CD;②AD=BC;③∠A=∠C;④AB=CD,现以其中的两个条件为一组,能判定四边形ABCD是平行四边形的条件有 ( )
A. 3组 B. 4组 C. 5组 D. 6组
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣(x﹣2)2+3的顶点坐标是( )
A.(﹣2,3)
B.(2,3)
C.(﹣2,﹣3)
D.(2,﹣3)
相关试题

