搜索
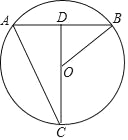
【题目】如图，点C在⊙O上，联结CO并延长交弦AB于点D， 
，联结AC、OB，若CD=40，AC=20
．
（1）求弦AB的长；
（2）求sin∠ABO的值．
参考答案：
【答案】（1）40；（2）
【解析】试题分析：（1）根据
，CD过圆心O，可得到CD⊥AB，AB=2AD=2BD，在Rt△ACD中利用勾股定理求得AD长即可得；
（2）利用勾股定理求得半径长，然后再根据正弦三角形函数的定义即可求得.
试题解析：（1）∵CD过圆心O， 
，
∴CD⊥AB，AB=2AD=2BD，
∵CD=40， 
，
又∵∠ADC=
，
∴
，
∴AB=2AD=40；
（2）设圆O的半径为r，则OD=40-r，
∵BD=AD=20， ∠ODB=
， ∴
，
∴
，
∴r=25，OD=15，
∴
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系
中，函数
的图像与函数
（
）的图像相交于点
，并与
轴交于点
．点
是线段
上一点，
与
的面积比为3：7．
（1）
_____，
_____．（2）求点
的坐标；（3）若将
绕点
逆时针旋转，得到
，其中点
落在轴负半轴上，判断点
是否落在函数（）的图像上，并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，小强从A处出发沿北偏东70°方向行走，走至B处，又沿着北偏西30°方向行走至C处，此时需把方向调整到与出发时一致，则方向的调整应是（ ）
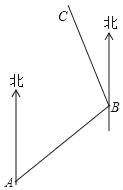
A. 左转 80° B. 右转80° C. 右转 100° D. 左转 100°
-
科目： 来源： 题型：
查看答案和解析>>【题目】（问题情境）
课外兴趣小组活动时，老师提出了如下问题：
（1）如图①，
中，
，若
，点
是斜边
上一动点，求线段
的最小值．
在组内经过合作交流，得到了如下的解决方法：
根据直线外一点和直线上各点连接的所有线段中，垂线段最短，得到：
当
时，线段取得最小值．请你根据小明的思路求出这个最小值．（思维运用）
（2）如图，在
中，，
，为斜边上一动点，过作
于点
，过作
于点
，求线段
的最小值．
（问题拓展）
（3）如图，
，
线段上的一个动点，分别以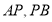
为边在的同侧作菱形
和菱形
，点
在一条直线上．
，
分别是对角线
的中点，当点在线段上移动时，点之间的距离的最小值为_____．（直接写出结果，不需要写过程）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一栋居民楼AB的高为16米，远处有一栋商务楼CD，小明在居民楼的楼底A处测得商务楼顶D处的仰角为
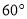，又在商务楼的楼顶D处测得居民楼的楼顶B处的俯角为
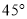．其中A、C两点分别位于B、D两点的正下方，且A、C两点在同一水平线上，求商务楼CD的高度．(参考数据：
， 
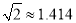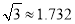.结果精确到0.1米)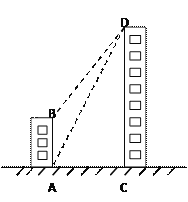
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在长方形ABCD中，AB＝8cm，BC＝6cm．点E是CD边上的一点，且DE＝2cm，动点P从A点出发，以2cm/s的速度沿A→B→C→E运动，最终到达点E.当△APE的面积等于20cm2时，则点P运动的时间为___________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直角坐标平面内，直线y=
x+2分别与x轴、y轴交于点A、C．抛物线y=﹣
+bx+c经过点A与点C，且与x轴的另一个交点为点B．点D在该抛物线上，且位于直线AC的上方．（1）求上述抛物线的表达式；
（2）联结BC、BD，且BD交AC于点E，如果△ABE的面积与△ABC的面积之比为4：5，求∠DBA的余切值；
（3）过点D作DF⊥AC，垂足为点F，联结CD．若△CFD与△AOC相似，求点D的坐标．
相关试题
