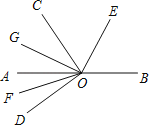
【题目】如图,O为直线AB上一点,∠DOC为直角,OE平分∠BOC,OF平分∠AOD,OG平分∠AOC,下列结论:①∠BOE与∠DOF互为余角;②2∠AOE﹣∠BOD=90°;③∠EOD与∠COG互为补角;④∠BOE﹣∠DOF=45°;其中正确的是( )
A.①②③④B.③④C.②③D.②③④
参考答案:
【答案】D
【解析】
根据余角和补角的定义以及角平分线的定义计算出各选项的结果判断即可.
解:∵OE平分∠BOC,OG平分∠AOC,
∴∠BOE+∠AOG=90°,
∵∠AOG≠∠DOF,
∴①错误;
∵∠DOC=∠GOE=90°,
∴∠AOE=135°﹣![]()
![]() ∠AOD,
∠AOD,
∴2∠AOE=270°﹣∠AOD,
∴2∠AOE﹣∠BOD=90°,
∴②正确;
∵∠DOC=∠GOE=90°,
∴∠EOD+∠COG=180°,
∴③正确;
∵OE平分∠BOC,OF平分∠AOD,
∴∠DOF+∠COG=45°,
∵OE平分∠BOC,OG平分∠AOC,
∴∠BOE+∠COG=90°,
∴∠BOE﹣∠DOF=45°;
∴④正确.
综上所述,正确的有②③④.
故选:D.
-
科目: 来源: 题型:
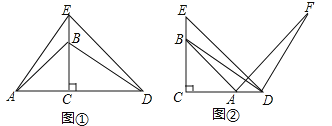
查看答案和解析>>【题目】已知△ABC与△DEC是两个大小不同的等腰直角三角形.
(1)如图①所示,连接AE,DB,试判断线段AE和DB的数量和位置关系,并说明理由;
(2)如图②所示,连接DB,将线段DB绕D点顺时针旋转90°到DF,连接AF,试判断线段DE和AF的数量和位置关系,并说明理由.
-
科目: 来源: 题型:
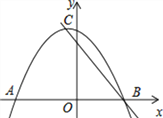
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣2,0)、B(x1,0),且1<x1<2,与y轴正半轴的交点在(0,2)的上方,顶点为C.直线y=kx+m(k≠0)经过点C、B.则下列结论:①b>a;②2a﹣b>﹣1;③2a+c<0;④k>a+b;⑤k<﹣1. 其中正确的结论有_________.(填序号)
-
科目: 来源: 题型:
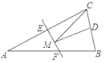
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为6,面积是24,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=80°,OC为从O点引出的任意一条射线,若OM平分∠AOC,ON平分∠BOC,则∠MON的度数是_____.
-
科目: 来源: 题型:
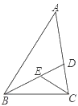
查看答案和解析>>【题目】①如图,在△ABC中,∠A=55°,∠ABD=32°,∠ACB=70°,且CE平分∠ACB,求∠DEC的度数.
②先化简再求值:化简:
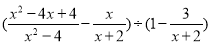 ,x=2020.
,x=2020. -
科目: 来源: 题型:
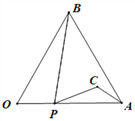
查看答案和解析>>【题目】如图,等边△AOB的边长为4,点P从点O出发,沿OA以每秒1个单位的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段BP的中点绕点P按顺时针方向旋转60°得点C,点C随点P的运动而运动,连接CP、CA.在点P从O向A运动的过程中,当△PCA为直角三角形时t的值为___________.
相关试题

