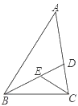
【题目】①如图,在△ABC中,∠A=55°,∠ABD=32°,∠ACB=70°,且CE平分∠ACB,求∠DEC的度数.
②先化简再求值:化简:![]() ,x=2020.
,x=2020.
参考答案:
【答案】①∠DEC=58°;②![]() .
.
【解析】
(1)先根据∠A=55°,∠ACB=70°得出∠ABC的度数,再由∠ABD=32°得出∠CBD的度数,根据CE平分∠ACB得出∠BCE的度数,最后用三角形的外角即可得出结论.
(2)先把括号内通分,再把除法转化为乘法,并把分子分母约分化简,然后把x=2020代入化简的结果计算即可.
①解:在△ABC中,
∵∠A=55°,∠ACB=70°
∴∠ABC=55°
∵∠ABD=32°,
∴∠CBD=∠ABC﹣∠ABD=23°
∵CE平分∠ACB,∴∠BCE=![]() ∠ACB=35°,
∠ACB=35°,
∴在△BCE中,∠DEC=∠CBD+BCE=58°.
②解:原式=![]()
=![]()
=![]()
当x=2020时,![]() =
=![]()
-
科目: 来源: 题型:
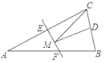
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为6,面积是24,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为_____.
-
科目: 来源: 题型:
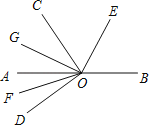
查看答案和解析>>【题目】如图,O为直线AB上一点,∠DOC为直角,OE平分∠BOC,OF平分∠AOD,OG平分∠AOC,下列结论:①∠BOE与∠DOF互为余角;②2∠AOE﹣∠BOD=90°;③∠EOD与∠COG互为补角;④∠BOE﹣∠DOF=45°;其中正确的是( )
A.①②③④B.③④C.②③D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=80°,OC为从O点引出的任意一条射线,若OM平分∠AOC,ON平分∠BOC,则∠MON的度数是_____.
-
科目: 来源: 题型:
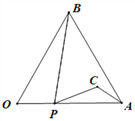
查看答案和解析>>【题目】如图,等边△AOB的边长为4,点P从点O出发,沿OA以每秒1个单位的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段BP的中点绕点P按顺时针方向旋转60°得点C,点C随点P的运动而运动,连接CP、CA.在点P从O向A运动的过程中,当△PCA为直角三角形时t的值为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017山东省莱芜市,第22题,10分)某网店销售甲、乙两种防雾霾口罩,已知甲种口罩每袋的售价比乙种口罩多5元,小丽从该网店网购2袋甲种口罩和3袋乙种口罩共花费110元.
(1)改网店甲、乙两种口罩每袋的售价各多少元?
(2)根据消费者需求,网店决定用不超过10000元购进价、乙两种口罩共500袋,且甲种口罩的数量大于乙种口罩的
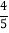 ,已知甲种口罩每袋的进价为22.4元,乙种口罩每袋的进价为18元,请你帮助网店计算有几种进货方案?若使网店获利最大,应该购进甲、乙两种口罩各多少袋,最大获利多少元?
,已知甲种口罩每袋的进价为22.4元,乙种口罩每袋的进价为18元,请你帮助网店计算有几种进货方案?若使网店获利最大,应该购进甲、乙两种口罩各多少袋,最大获利多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

相关试题

