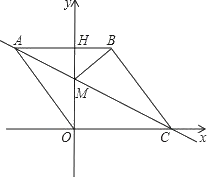
【题目】如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在![]() 轴的正半轴上,直线AC交
轴的正半轴上,直线AC交![]() 轴于点M,AB边交
轴于点M,AB边交![]() 轴于点H,连接BM.
轴于点H,连接BM.
(1)求菱形ABCO的边长; (2)求直线AC的解析式.
参考答案:
【答案】(1)5;(2)![]()
【解析】
(1)过点A作AE![]() 于E,由点A坐标得AE,OE长度,通过勾股定理得AO长度,得出结果;
于E,由点A坐标得AE,OE长度,通过勾股定理得AO长度,得出结果;
(2)由菱形性质得出OC=OA,得出点C坐标,用待定系数法完成计算即可.
(1)过点A作AE![]() 于E,如图所示:
于E,如图所示:
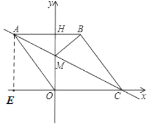
由点A(![]() ),得AE=4,OE=3
),得AE=4,OE=3
∴![]()
所以菱形ABCO的边长为5.
(2)由ABCO为菱形,
∴OC=OA=5
∵点C在![]() 轴上
轴上
∴C(5.0)
设直线![]() 的解析式为:
的解析式为:![]()
则![]() ,解得
,解得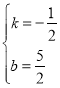
所以直线![]() 的解析式为:
的解析式为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,横、纵坐标均为整数的点叫做整数点,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题:
(1)填表:
点P从O点出发的时间
可以到达的整坐标
可以到达整数点的个数
1秒
(0,1),(1,0)
2
2秒
(0,2),(2,0),(1,1)
3
3秒
( )
( )
(2)当点P从点O出发10秒,可到达的整数点的个数是____________个;
(3)当点P从O点出发____________秒时,可得到整数点(10,5).
-
科目: 来源: 题型:
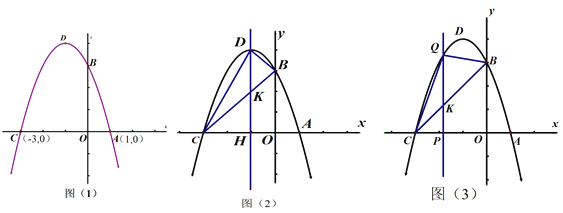
查看答案和解析>>【题目】已知,如图,抛物线与x轴交点坐标为A(1,0),C(-3,0),
(1)若已知顶点坐标D为(-1,4)或B点(0,3),选择适当方式求抛物线的解析式.
(2)若直线DH为抛物线的对称轴,在(1)的基础上,求线段DK的长度,并求△DBC的面积.
(3)将图(2)中的对称轴向左移动,交x轴于点p(m,0)(-3<m<-1),与线段BC、抛物线的交点分别为点K、Q,用含m的代数式表示QK的长度,并求出当m为何值时,△BCQ的面积最大?
-
科目: 来源: 题型:
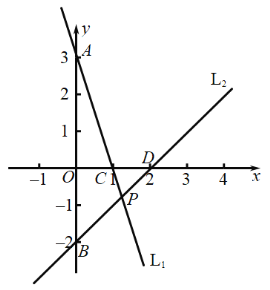
查看答案和解析>>【题目】如图,L1、L2分别表示两个一次函数的图象,它们相交于点P.
(1)求出两条直线的函数关系式;
(2)点P的坐标可看作是哪个二元一次方程组的解?
(3)求出图中△APB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是48cm,求:
(1)两条对角线的长度;
(2)菱形的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项,现随机抽查了m名学生,并将其结果绘制成如下不完整的条形图和扇形图.

请结合以上信息解答下列问题:
(1)m= ;
(2)请补全上面的条形统计图;
(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为 ;
(4)已知该校共有1200名学生,请你估计该校约有 名学生最喜爱足球活动.
相关试题

