【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②b24ac<0;③4a+c>2b;④(a+c)2>b2;⑤x(ax+b)ab其中正确结论的是___.
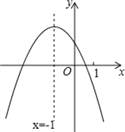
A. ①②⑤ B. ②③④ C. ①③⑤ D. ③④⑤
参考答案:
【答案】C
【解析】分析:①根据抛物线的开口方向确定a的符号,与y轴的交点确定c的符号,对称轴在y轴的左侧确定b的符号;②由抛物线与x轴的交点的个数确定;③判断当x=-2时的函数值;④判断当x=-1时,a+c与b的关系,注意b的符号;⑤当x=-1时,函数取最大值,所以ax2+bx+c≤a-b+c.
详解:①因为抛物线开口向下,所以a<0;
因为抛物线与y轴交点在y轴的正半轴上,所以c>0;
因为对称轴x=![]() =-1,即b=2a,而a<0,所以b<0,
=-1,即b=2a,而a<0,所以b<0,
所以abc>0.
则①正确;
②因为抛物线与x轴有两个交点,所以b24ac>0.
则②错误;
③因为对称轴x=-1,所以坐标(-2,0)的点与(0,0)关于x=-1对称.
所以当x=-2时,(-2)2a+(-2)b+c>,即4a-2b+c>0,所以4a+c>2b.
则③正确;
④因为当x=-1时,a-b+c>0,所以a+c>b,但b<0,则不能确定(a+c)2与b2的大小.
则④不正确;
⑤当x=-1时,y有最大值是y=a-b+c,
所以ax2+bx+c≤a-b+c,即x(ax+b)≤a-b.
则⑤正确.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
(1)求抛物线的解析式;
(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
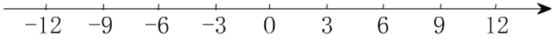
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】瞳瞳做一道数学题:求代数式
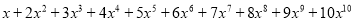 当x=-1时的值,由于瞳瞳粗心把式子中的某一项前的“+”号错误地看成了“—”号,算出代数式的值是-11,那么瞳瞳看错的是 次项前的符号,写出x=-1和x=1时代数式的值.
当x=-1时的值,由于瞳瞳粗心把式子中的某一项前的“+”号错误地看成了“—”号,算出代数式的值是-11,那么瞳瞳看错的是 次项前的符号,写出x=-1和x=1时代数式的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】进入初中的学习,除了代数中学习了新的概念有理数,也开始了几何初步的学习,并且老师强调几何内容必须带齐作图工具,初一年级的学生沟通后觉得到网上买作图工具更方便更优惠些,一套如图的作图工具是2.3元/套,如果一次买100套以上(不含100套),售价是2.2元/套.
(1)列式表示买n套这样的作图工具所需钱数(注意对n的大小要有所考虑)
(2)按照这样的售价规定,会不会出现多买比少买反而付钱少的情况?
(3)如果需要买100套,怎样买更省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】分类讨论是一种非常重要的数学方法,如果一道题提供的已知条件中包含几种情况,我们可以分情况讨论来求解.例如:若
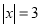 ,
, 求
求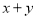 的值.
的值.情况若x=3,y=2时,
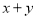 =5
=5情况若x=3,y=-2时,
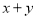 =1
=1情况③若x=-3,y=2时,
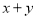 =-1
=-1情况④若x=-3,y=-2时,
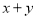 =-5
=-5所以,
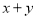 的值为1,-1,5,-5.
的值为1,-1,5,-5.几何的学习过程中也有类似的情况:
如图,点O是直线AB上的一点,将一直角三角板如图摆放,过点O作射线OE平分
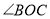 .当直角三角板绕点O继续顺时针旋转一周回到图1的位置时,在旋转过程中你发现
.当直角三角板绕点O继续顺时针旋转一周回到图1的位置时,在旋转过程中你发现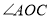 与∠DOE(
与∠DOE(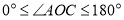 ,
,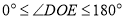 )之间有怎样的数量关系?
)之间有怎样的数量关系?情况(1)如图1,当
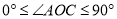 时,若
时,若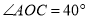 ,则∠DOE度数是
,则∠DOE度数是 情况(2)如图2,当∠AOC是钝角时,使得直角边OC在直线AB的上方,若∠AOC=160°,其他条件不变,则∠DOE的度数是
情况(3)若
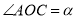 ,在旋转过程中你发现
,在旋转过程中你发现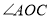 与∠DOE之间有怎样的数量关系?请你直接用含α的代数式表示∠DOE的度数;
与∠DOE之间有怎样的数量关系?请你直接用含α的代数式表示∠DOE的度数;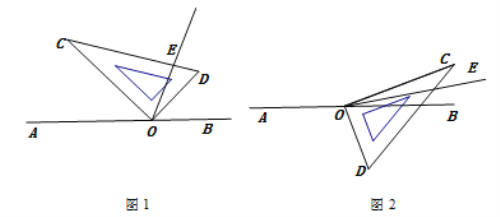
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)分解因式:m2(x﹣y)+4n2(y﹣x);
(2)解不等式组
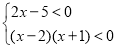 ,并把解集在数轴上表示出来;
,并把解集在数轴上表示出来;(3)先化简,再求解,
 ,其中x=
,其中x=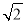 ﹣2.
﹣2.
相关试题

