【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BCAD=![]() AE2;④∠DFE=2∠DAC ;⑤若连接CH,则CH∥EF.其中正确的个数为( )
AE2;④∠DFE=2∠DAC ;⑤若连接CH,则CH∥EF.其中正确的个数为( )

A. 2个 B. 3个 C. 4个 D. 5个
参考答案:
【答案】D
【解析】试题解析:∵在△ABC中,AD和BE是高,
∴∠ADB=∠AEB=∠CEB=90°,
∵点F是AB的中点,
∴FD=![]() AB,
AB,
∵∠ABE=45°,
∴△ABE是等腰直角三角形,
∴AE=BE,
∵点F是AB的中点,
∴FE=![]() AB,
AB,
∴FD=FE,①正确;
∵∠CBE=∠BAD,∠CBE+∠C=90°,∠BAD+∠ABC=90°,
∴∠ABC=∠C,
∴AB=AC,
∵AD⊥BC,
∴BC=2CD,∠BAD=∠CAD=∠CBE,
在△AEH和△BEC中,
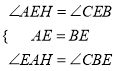 ,
,
∴△AEH≌△BEC(ASA),
∴AH=BC=2CD,②正确;
∵∠BAD=∠CBE,∠ADB=∠CEB,
∴△ABD~△BCE,
∴![]() ,即BCAD=ABBE,
,即BCAD=ABBE,
∵![]() AE2=ABAE=ABBE,
AE2=ABAE=ABBE,
∴BCAD=![]() AE2;③正确;
AE2;③正确;
∵F是AB的中点,BD=CD,
∴S△ABC=2S△ABD=4S△ADF.④正确;
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大正方形的边长为a,小正方形的边长为b,

(1)用代数式表示阴影部分的面积;
(2)当a=10cm,b=4cm时,求阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据等式和不等式的性质,可以得到:若a﹣b>0,则a>b;若a﹣b=0,则a=b;若a﹣b<0,则a<b.这是利用“作差法”比较两个数或两个代数式值的大小.
(1)试比较代数式5m2﹣4m+2与4m2﹣4m﹣7的值之间的大小关系;
解:(5m2﹣4m+2)﹣(4m2﹣4m﹣7)=5m2﹣4m+2﹣4m2+4m+7=m2+9,因为m2≥0
所以m2+9>0
所以5m2﹣4m+24m2﹣4m﹣7.(用“>”或“<”填空)
(2)已知A=5m2﹣4( m﹣
m﹣  ),B=7(m2﹣m)+3,请你运用前面介绍的方法比较代数式A与B的大小.
),B=7(m2﹣m)+3,请你运用前面介绍的方法比较代数式A与B的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】长城总长约为6700000,用科学记数法表示为
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列6个结论正确的有________个.
①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意x均有ax2+bx≥a+b;⑤3a+c=0;⑥b+2c<0;⑦当x>1时,y随着x的增大而减小
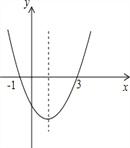
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
2(x2y+xy)﹣3(x2y﹣xy)﹣4x2y,其中x=1,y=﹣1. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个数的平方和它的倒数相等,则这个数是( )
A.1
B.﹣1
C.±1
D.±1和0
相关试题

