Question

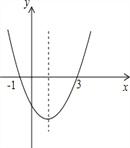
【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列6个结论正确的有________个.

①ac<0；②2a+b=0；③4a+2b+c>0；④对于任意x均有ax2+bx≥a+b；⑤3a+c=0；⑥b+2c<0；⑦当x>1时，y随着x的增大而减小

Answer 1

【答案】5

【解析】①∵图象过点（-1，0），（3，0），∴对称轴为x=1，

∵抛物线的开口向上，∴a＞0，

∵与y轴的交点为在y轴的负半轴上，∴c＜0，

∵对称轴为x=>0 ,

∴a、b异号，即b＜0，

∴ac＜0，故①是正确的;

②2a+b=0，

∵对称轴为x=1，

∴x= ,

∴-b=2a，

∴2a+b=0，故②是正确的;

③当x=2时，y=4a+2b+c＜0，此③是错误的；

④对于任意x均有ax2+ax＞a+b，

当x=-1，则a-a=0，

∵2a+b=0，

∴a+b＜0，

∴ax2+ax＞a+b，

当x=0，则a+b＜0，

∴ax2+ax＞a+b，

当x=1，则a+a=2a，

∵2a+b=0，

∴a+b＜0，

2a＞a+b，

∴ax2+ax＞a+b,故④是正确的;

⑤抛物线对称轴x== , 则b=-2a,

如图，当x=-1时，y=0，即a-b+c=3a+c=0，故⑤正确的；

⑥∵函数的图象与y轴负半轴相交一点,

∴c<0,

又∵由①可知:b<0,

∴b+2c<0,故⑥正确；

⑦如图所示:当x>1时，y随着x的增大而增大,故⑦是错误的;

综合上述可得:①②④⑤⑥共5个正确的;

故答案是5.

点睛: 二次函数y=ax2+bx+c（a≠0），二次项系数a决定抛物线的开口方向和大小:当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时（即ab＞0），对称轴在y轴左边； 当a与b异号时（即ab＜0），对称轴在y轴右边；常数项c决定抛物线与y轴交点:抛物线与y轴交于（0，c）；抛物线与x轴交点个数由△决定:当△=b2-4ac＞0时，抛物线与x轴有2个交点；当△=b2-4ac=0时，抛物线与x轴有1个交点；当△=b2-4ac＜0时，抛物线与x轴没有交点.