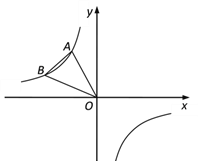
【题目】如图,点A、B在反比例函数y=- ![]() 的图象上,且点A、B的横坐标分别为a、2a(a<0).
的图象上,且点A、B的横坐标分别为a、2a(a<0).
(1)求△AOB的面积;
(2)若点C在x轴上,点D在y轴上,且四边形ABCD为正方形,求a的值.
参考答案:
【答案】(1)3;(2)a=- ![]()
【解析】试题分析:![]() 作AM⊥x轴于M,BN⊥x轴于N,设AM交OB于点E, S△AOM =S△BON, S△AOE =S梯形BEMN ,得到S△AOB =S梯形BAMN,求出梯形的面积即可.
作AM⊥x轴于M,BN⊥x轴于N,设AM交OB于点E, S△AOM =S△BON, S△AOE =S梯形BEMN ,得到S△AOB =S梯形BAMN,求出梯形的面积即可.
![]() 作BE⊥x轴于E,证明Rt△EBC≌Rt△OCD,
作BE⊥x轴于E,证明Rt△EBC≌Rt△OCD,![]()
列出式子![]() 求解即可.
求解即可.
试题解析:![]() 作AM⊥x轴于M,BN⊥x轴于N,设AM交OB于点E,
作AM⊥x轴于M,BN⊥x轴于N,设AM交OB于点E,
则S△AOM =S△BON,
∴S△AOE =S梯形BEMN ,∴S△AOB =S梯形BAMN
由题意知,![]()
![]()
![]()
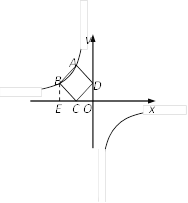
(2)作BE⊥x轴于E,
∵四边形ABCD为正方形,∴BC=CD,∠BCD=90°,
∴∠BCE+∠OCD=90°,
又∠BCE+∠EBC=90°,∴∠EBC=∠OCD,
∴Rt△EBC≌Rt△OCD,
∴BE=CO,
又![]() 点C在x轴上,点D在y轴上
点C在x轴上,点D在y轴上
![]()
![]()

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展爱“我容城,创卫同行”的活动,倡议学生利用双休日在浜江公园参加评选活动,为了了解同学们劳动时间,学校随机调查了部分同学劳动的时间,并用得到的数据绘制了不完整的统计图,根据图中信息解答下列问题:
(1)将条形统计图补充完整;
(2)抽查的学生劳动时间的众数为______,中位数为_______;
(3)已知全校学生人数为1200人,请估算该校学生参加义务劳动2小时的有多少人?

-
科目: 来源: 题型:
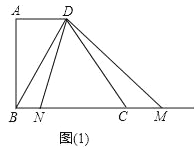
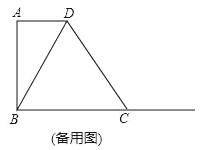
查看答案和解析>>【题目】已知,在梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=4,BC=5,在射线BC任取一点M,联结DM,作∠MDN=∠BDC,∠MDN的另一边DN交直线BC于点N(点N在点M的左侧).
(1)当BM的长为10时,求证:BD⊥DM;
(2)如图(1),当点N在线段BC上时,设BN=x,BM=y,求y关于x的函数关系式,并写出它的定义域;
(3)如果△DMN是等腰三角形,求BN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市区自2014年1月起,居民生活用水开始实行阶梯式计量水价,该阶梯式计量水价分为三级(如下表所示):
月用水量(吨)
水价(元/吨)
第一级 20吨以下(含20吨)
1.6
第二级 20吨﹣30吨(含30吨)
2.4
第三级 30吨以上
3.2
例:某用户的月用水量为32吨,按三级计量应缴水费为:
1.6×20+2.4×10+3.2×2=62.4(元)
(1)如果甲用户的月用水量为12吨,则甲需缴的水费为 元;
(2)如果乙用户缴的水费为39.2元,则乙月用水量 吨;
(3)如果丙用户的月用水量为a吨,则丙用户该月应缴水费多少元?(用含a的代数式表示,并化简)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”。图中点A表示-10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位,动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速,设运动的时间为t秒,问:
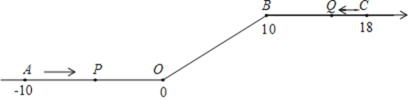
(1)动点P从点A运动至点C需要________秒;
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少?
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
-
科目: 来源: 题型:
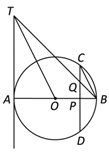
查看答案和解析>>【题目】如图,AB是⊙O的直径,AT是经过点A的切线,弦CD垂直AB于P点,Q为线段CP的中点,连接BQ并延长交切线AT于T点,连接OT.
(1)求证:BC∥OT;
(2)若⊙O直径为10,CD=8,求AT的长;
(3)延长TO交直线CD于R,若⊙O直径为10,CD=8,求TR的长.
相关试题

