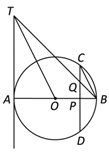
【题目】如图,AB是⊙O的直径,AT是经过点A的切线,弦CD垂直AB于P点,Q为线段CP的中点,连接BQ并延长交切线AT于T点,连接OT.
(1)求证:BC∥OT;
(2)若⊙O直径为10,CD=8,求AT的长;
(3)延长TO交直线CD于R,若⊙O直径为10,CD=8,求TR的长.
参考答案:
【答案】(1)证明见解析;(2)10;(3)8![]()
【解析】试题分析:(1)此题要通过构造相似三角形求解,由于P是CD的中点,由垂径定理知CD⊥AB,有切线的性质可得:AT⊥AB,由此可证得AT∥CD,得![]() 取PB的中点E,则
取PB的中点E,则![]() 又因为
又因为![]() 等量代换后可证得
等量代换后可证得![]() 由此可得△TAO∽△QPE,根据相似三角形所得的等角,可证得OT∥QE,而QE是
由此可得△TAO∽△QPE,根据相似三角形所得的等角,可证得OT∥QE,而QE是![]() 的中位线,则 QE∥BC,根据平行线的传递性即可证得BC∥OT.
的中位线,则 QE∥BC,根据平行线的传递性即可证得BC∥OT.
(2)(3)题可利用△TAO∽△CPB,求出AT和OT的值,再利用△AOT∽△POR求出OR的值,从而解决问题.
试题解析:(1)证明:取PB的中点E,连接QE,
∵Q是PC的中点,E是PB的中点,
∴QE为△PBC的中位线,QE∥BC,
∵AT为经过A点的切线,AB为直径,
∴AT⊥AB,
∵CD⊥AB,∴AT∥CD,∠TAO=∠QPE=90°,
∴△BPQ∽△BAT,![]()
∵PB=2PE,AB=2AO,![]()
∴△TAO∽△QPE,∴∠AOT=∠PEQ,
∴OT∥QE,
∵QE∥BC,∴BC∥OT .
(2)∵CD⊥AB,AB为直径,CD=8,
∴CP=PD=4,
连接OC,
在Rt△OCP中,∵PC=4,![]()
∴OP=3,∴PB=OB-OP=2,
BC∥OT,∴△TAO∽△CPB,![]()
∵![]()
∴AT=10,
(3)解:在Rt△TAO中,![]()
∵AT∥CR,∴△AOT∽△POR,
![]()
∴![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B在反比例函数y=-
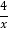 的图象上,且点A、B的横坐标分别为a、2a(a<0).
的图象上,且点A、B的横坐标分别为a、2a(a<0).(1)求△AOB的面积;
(2)若点C在x轴上,点D在y轴上,且四边形ABCD为正方形,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”。图中点A表示-10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位,动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速,设运动的时间为t秒,问:
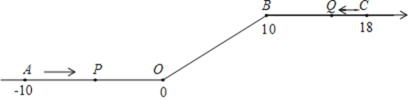
(1)动点P从点A运动至点C需要________秒;
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少?
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=
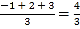 ,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
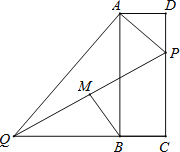
(1)求证:△ADP∽△ABQ;
(2)若AD=10,AB=20,点P在边CD上运动,设DP=x,BM2=y,求y与x的函数关系式,并求线段BM的最小值;
(3)若AD=10,AB=a,DP=8,随着a的大小的变化,点M的位置也在变化.当点M落在矩形ABCD外部时,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图22,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E是边AB上的—个动点(不与点A、N重合),过点E的反比例函数
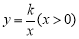 的图象与边BC交于点F。
的图象与边BC交于点F。【1】若△OAE、△OCF的而积分别为S1、S2.且S1+S2=2,求
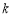 的值:
的值:【2】若OA=2.0C=4.问当点E运动到什么位置时,四边形OAEF的面积最大.其最大值为多少?
相关试题

