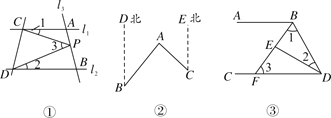
【题目】(1)如图①,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在线段AB上,则∠1,∠2,∠3之间的等量关系是____;
(2)如图②,点A在B处北偏东40°方向,在C处北偏西45°方向,则∠BAC=____°.
(3)如图③,∠ABD和∠BDC的平分线交于点E,BE交AB于点F,∠1+∠2=90°,试说明:AB∥AB,并探究∠2与∠3的数量关系.
参考答案:
【答案】(1)∠1+∠2=∠3(2)85(3)见解析,∠2+∠3=90°
【解析】
(1)作PM∥AC.根据平行线间的传递性,得PM∥BD.再由平行线的性质,得∠1=∠CPM,∠2=∠MPD.所以,∠1+∠2=∠3.(2)由题可知∠BAC=∠B+∠C,所以,∠BAC=85°.(3)由题意,先证明AB∥AB.再通过角的变换,得到∠BED=∠DAB=90°,所以∠3+∠FDE=90![]() ,最后得到∠2+∠3=90.
,最后得到∠2+∠3=90.
(1)如答图,作PM∥AC,
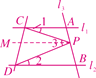
∵AC∥BD,∴PM∥BD,
∴∠1=∠CPM,∠2=∠MPD,
∴∠1+∠2=∠CPM+∠MPD=∠CPD=∠3.
(2)由题可知∠BAC=∠B+∠C.
∵∠B=40°,∠C=45°,
∴∠BAC=40°+45°=85°.
(3)证明:∵BE,DE分别平分∠ABD,∠BDC,
∴∠1=![]() ∠ABD,∠2=
∠ABD,∠2=![]() ∠BDC.
∠BDC.
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°,
∴AB∥AB.
∵DE平分∠BDC,
∴∠2=∠FDE.
∵∠1+∠2=90°,
∴∠BED=∠DAB=90°,
∴∠3+∠FDE=90°,
∴∠2+∠3=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.
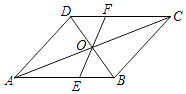
(1)求证:OE=OF;
(2)若AB=6,BC=5,OE=2,求四边形BCFE的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张在甲楼A处向外看,由于受到前面乙楼的遮挡,最近只能看到地面D处,俯角为α.小颖在甲楼B处(B在A的正下方)向外看,最近能看到地面E处,俯角为β,地面上G,F,D,E在同一直线上,已知乙楼高CF为10m,甲乙两楼相距FG为15m,俯角α=45°,β=35°.
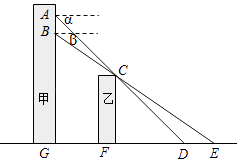
(1)求点A到地面的距离AG;
(2)求A,B之间的距离.(结果精确到0.1m)
(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70) -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,横、纵坐标都为整数的点称为整点.如图,从内向外依次为第
 ,
, ,
, ,
, ,
, 个正方形(实线),若整点
个正方形(实线),若整点 在第
在第 个正方形的边上,则
个正方形的边上,则 ,
, ,
, 之间满足的数量关系为_______.
之间满足的数量关系为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,分别把两个边长为
 的小正方形沿一条对角线裁成
的小正方形沿一条对角线裁成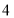 个小三角形拼成一个大正方形,则大正方形的边长为_______
个小三角形拼成一个大正方形,则大正方形的边长为_______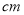 ;
;
(2)若一个圆的面积与一个正方形的面积都是
 ,设圆的周长为
,设圆的周长为 ,正方形的周长为
,正方形的周长为 ,则
,则 _____
_____ (填“
(填“ ”或“
”或“ ”或“
”或“ ”号);
”号);(3)如图,若正方形的面积为
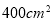 ,李明同学想沿这块正方形边的方向裁出一块面积为
,李明同学想沿这块正方形边的方向裁出一块面积为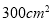 的长方形纸片,使它的长和宽之比为
的长方形纸片,使它的长和宽之比为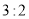 ,他能裁出吗?请说明理由?
,他能裁出吗?请说明理由?
相关试题

