【题目】解方程:x2﹣4x+3=0.
参考答案:
【答案】解法一:移项得 x2﹣4x=﹣3,
配方得 x2﹣4x+4=﹣3+4,
∴(x﹣2)2=1,
即 x﹣2=1或x﹣2=﹣1,
∴x1=3,x2=1;
解法二:∵a=1,b=﹣4,c=3,
∴b2﹣4ac=(﹣4)2﹣4×1×3=4>0,
∴ ![]() ,
,
∴x1=3,x2=1;
解法三:原方程可化为 (x﹣1)(x﹣3)=0,
∴x﹣1=0或x﹣3=0,
∴x1=1,x2=3.
【解析】此题可以采用配方法:首先将常数项3移到方程的左边,然后再在方程两边同时加上4,即可达到配方的目的,继而求得答案;
此题也可采用公式法:注意求根公式为把x= ![]() ,解题时首先要找准a,b,c;
,解题时首先要找准a,b,c;
此题可以采用因式分解法,利用十字相乘法分解因式即可达到降幂的目的.
【考点精析】关于本题考查的配方法和公式法,需要了解左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题;要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②AE=AF;③∠EBC=∠C;④FG∥AC;⑤EF=FG.其中正确的结论是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于(﹣2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是( )

A.x<﹣2
B.x>4
C.﹣2<x<4
D.x>0 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知一个多边形的内角和是它的外角和的 3 倍,求这个多边形的边数.
(2)如图,点F 是△ABC 的边 BC 延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF 的度数.
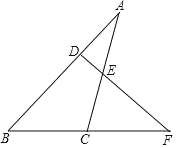
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).

(1)画出点B关于点A的对称点B1 , 并写出点B1的坐标;
(2)画出△ABC绕点C逆时针旋转90°后的图形△A′B′C,并写出点B的对应点B′的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+2x+2k﹣2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若k为正整数,求该方程的根. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
(1)描出A(﹣4,3)、B(﹣1,0)、C(﹣2,3)三点.
(2)△ABC 的面积是多少?
(3)作出△ABC 关于 y 轴的对称图形.
(4)请在x 轴上求作一点P,使△PA1C1 的周长最小,并直接写出点P 的坐标
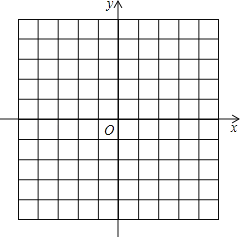
相关试题

