【题目】已知关于x的一元二次方程x2+2x+2k﹣2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若k为正整数,求该方程的根.
参考答案:
【答案】
(1)解:∵关于x的一元二次方程x2+2x+2k﹣2=0有两个不相等的实数根,
∴△>0,
∴△=22﹣4(2k﹣2)=4﹣8k+8=12﹣8k,
∴12﹣8k>0,
∴k< ![]()
(2)解:∵k< ![]() ,并且k为正整数,
,并且k为正整数,
∴k=1,
∴该方程为x2+2x=0,
∴该方程的根为x1=0,x2=﹣2
【解析】(1)根据一元二次方程x2+2x+2k﹣2=0有两个不相等的实数根可得△=22﹣4(2k﹣2)=4﹣8k+8=12﹣8k>0,求出k的取值范围即可;(2)根据k的取值范围,结合k为正整数,得到k的值,进而求出方程的根.
【考点精析】掌握求根公式是解答本题的根本,需要知道根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知一个多边形的内角和是它的外角和的 3 倍,求这个多边形的边数.
(2)如图,点F 是△ABC 的边 BC 延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF 的度数.
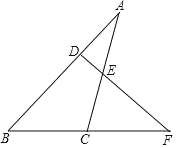
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2﹣4x+3=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).

(1)画出点B关于点A的对称点B1 , 并写出点B1的坐标;
(2)画出△ABC绕点C逆时针旋转90°后的图形△A′B′C,并写出点B的对应点B′的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
(1)描出A(﹣4,3)、B(﹣1,0)、C(﹣2,3)三点.
(2)△ABC 的面积是多少?
(3)作出△ABC 关于 y 轴的对称图形.
(4)请在x 轴上求作一点P,使△PA1C1 的周长最小,并直接写出点P 的坐标
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD、CE. 求证:BD=CE.
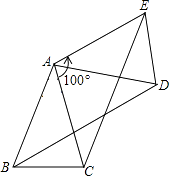
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B=50°,P 为 AB 中点,点 M 为射线 AC 上(不与点 A 重合)的任意一点,连接 MP, 并使MP 的延长线交射线BD 于点N,设∠BPN=α.

(1)求证:△APM≌△BPN;
(2)当 MN=2BN 时,求α的度数;
(3)若△BPN 为锐角三角形时,直接写出α的取值范围.
相关试题

