【题目】如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.
(1)求证:△AFE≌ODFB;
(2)求证:四边形ADCE是平行四边形;
(3)当AB、AC之间满足什么条件时,四边形ADCE是矩形.

参考答案:
【答案】(1)见解析;(2)见解析;(3)当AB=AC时,四边形ADCE是矩形.
【解析】
(1)根据“AAS”即可证明△AFE≌△DFB;
(2)由△AFE≌△DFB可证明AE=CD,再由AE∥BC可利用一组对边平行且相等的四边形是平行四边形可得四边形ADCE是平行四边形;
(2)当AB=AC时,根据等腰三角形三线合一可得AD⊥BC,再根据有一个角是直角的平行四边形是矩形可得结论.
(1)∵AE∥BC,
∴∠AEF=∠DBF ,
∵∠AFE=∠DFB,AF=DF,
∴△AFE≌△DFB(AAS);
(2)∵△AFE≌△DFB,
∴AE=BD,
∵AD是△ABC的中线,
∴BD=CD,
∴AE=CD ,
∵AE∥BC,
∴四边形ADCE是平行四边形;
(3)当AB=AC时,四边形ADCE是矩形;
∵AB=AC,AD是△ABC的中线,
∴AD⊥BC,
∴∠ADC=90°
∵四边形ADCE是平行四边形,
∴四边形ADCE是矩形,
∴当AB=AC时,四边形ADCE是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点
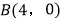 、
、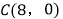 、
、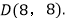 抛物线
抛物线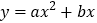 过A、C两点.
过A、C两点. 直接写出点A的坐标,并求出抛物线的解析式;
直接写出点A的坐标,并求出抛物线的解析式; 动点P从点A出发
动点P从点A出发 沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动
沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动 速度均为每秒1个单位长度,运动时间为t秒
速度均为每秒1个单位长度,运动时间为t秒 过点P作
过点P作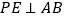 交AC于点E.
交AC于点E. 过点E作
过点E作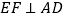 于点F,交抛物线于点
于点F,交抛物线于点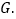 当t为何值时,线段EG最长?
当t为何值时,线段EG最长? 连接
连接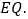 在点P、Q运动的过程中,判断有几个时刻使得
在点P、Q运动的过程中,判断有几个时刻使得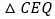 是等腰三角形?请直接写出相应的t值.
是等腰三角形?请直接写出相应的t值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】高斯上小学时,有一次数学老师让同学们计算“从1到100这100个正整数的和”.许多同学都采用了依次累加的计算方法,计算起来非常繁琐,且易出错.聪明的小高斯经过探索后,给出了下面漂亮的解答过程.
解:设S=1+2+3+…+100 ①
则S=100+99+98+…+1 ②
①+②,得(即左右两边分别相加):
2S=(1+100)+(2+99)+(3+98)+…+(100+1),
=
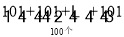 ,
,=100×101,
所以,S=
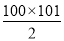 ③,
③,所以,1+2+3+…+100=5050.
后来人们将小高斯的这种解答方法概括为“倒序相加法”.请你利用“倒序相加法”解答下面的问题.
(1)计算:1+2+3+…+101;
(2)请你观察上面解答过程中的③式及你运算过程中出现的类似③式,猜想:1+2+3+…+n= ;
(3)至少用两种方法计算:1001+1002+…+2000.
方法1:
方法2:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
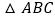 中,
中,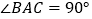 ,
,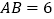 ,
, ,点D是BC的中点,将
,点D是BC的中点,将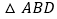 沿AD翻折得到
沿AD翻折得到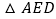 ,联结CE,那么线段CE的长等于_______.
,联结CE,那么线段CE的长等于_______.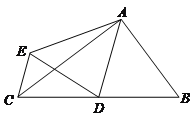
-
科目: 来源: 题型:
查看答案和解析>>【题目】温度通常有两种表示方法:华氏度(单位:℉)与摄氏度(单位:℃),已知华氏度数
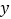 与摄氏度数
与摄氏度数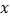 之间是一次函数关系,下表列出了部分华氏度与摄氏度之间的对应关系:
之间是一次函数关系,下表列出了部分华氏度与摄氏度之间的对应关系:摄氏度数
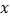 (℃)
(℃)…
0
…
35
…
100
…
华氏度数
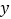 (℉)
(℉)…
32
…
95
…
212
…
(1)选用表格中给出的数据,求y关于x的函数解析式;
(2)有一种温度计上有两个刻度,即测量某一温度时左边是摄氏度,右边是华氏度,那么在多少摄氏度时,温度计上右边华氏度的刻度正好比左边摄氏度的刻度大56?
-
科目: 来源: 题型:
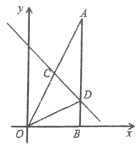
查看答案和解析>>【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,直线y=-x+b分别交OA、AB于点C、D,且ΔBOD的面积是4.
(1)求直线AO的解析式;
(2)求直线CD的解析式;
(3)若点M是x轴上的点,且使得点M到点A和点C的距离之和最小,求点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
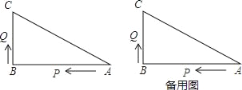
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
相关试题

