搜索
【题目】为实施乡村振兴战略，解决某山区老百姓出行难的问题，当地政府决定修建一条高速公路.其中一段长为146米的山体隧道贯穿工程由甲乙两个工程队负责施工.甲工程队独立工作2天后，乙工程队加入，两工程队又联合工作了1天，这3天共掘进26米.已知甲工程队每天比乙工程队多掘进2米，按此速度完成这项隧道贯穿工程，甲乙两个工程队还需联合工作多少天？
参考答案：
【答案】甲乙两个工程队还需联合工作10天.
【解析】
设甲工程队每天掘进x米，则乙工程队每天掘进（x-2）米，利用甲、乙两工程队3天共掘进26米列出方程，分别求得甲、乙工程队每天的工作量，再求出结果即可.
解：设甲工程队每天掘进x米，则乙工程队每天掘进（x-2）米，
由题意得2x+（x+x-2）=26，解得x=7，所以乙工程队每天掘进5米，
（天）
答：甲乙两个工程队还需联合工作10天
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）（-12）-5+（-14）-（-39） （2）
（3）5(a2b－ab2)－(ab2＋3a2b) （4）
（用简便方法计算） -
科目： 来源： 题型：
查看答案和解析>>【题目】由几个相同的边长为1的小立方块搭成的几何体的俯视图如下图，格中的数字表示该位置的小立方块的个数．
(1)请在下面方格纸中分别画出这个向何体的主视图和左视图．
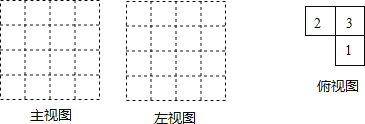
(2)根据三视图；这个组合几何体的表面积为 _________ 个平方单位．(包括底面积)
(3)若上述小立方块搭成的几何体的俯视图不变，各位置的小立方块个数可以改变(总数目不变)，则搭成这样的组合几何体中的表面积最大是为 _________ 个平方单位．(包括底面积)
-
科目： 来源： 题型：
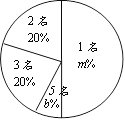
查看答案和解析>>【题目】为了有效地落实国家精准扶贫政策，切实关爱贫困家庭学生．某校对全校各班贫困家庭学生的人数情况进行了调查．发现每个班级都有贫困家庭学生，经统计班上贫困家庭学生人数分别有1名、2名、3名、5名，共四种情况，并将其制成了如下两幅不完整的统计图：
(1)填空：a = ，b= ；
(2)求这所学校平均每班贫困学生人数；
(3)某爱心人士决定从2名贫困家庭学生的这些班级中，任选两名进行帮扶，请用列表或画树状图的方法，求出被选中的两名学生来自同一班级的概率．
贫困学生人数
班级数
1名
5
2名
2
3名
a
5名
1
-
科目： 来源： 题型：
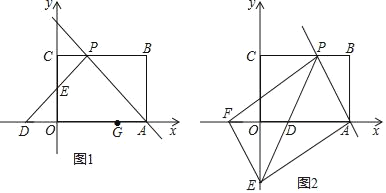
查看答案和解析>>【题目】如图1，矩形OABC摆放在平面直角坐标系中，点A在x轴上，点C在y轴上，OA＝3，OC＝2，过点A的直线交矩形OABC的边BC于点P，且点P不与点B、C重合，过点P作∠CPD＝∠APB，PD交x轴于点D，交y轴于点E．
(1)若△APD为等腰直角三角形．
①求直线AP的函数解析式；
②在x轴上另有一点G的坐标为(2，0)，请在直线AP和y轴上分别找一点M、N，使△GMN的周长最小，并求出此时点N的坐标和△GMN周长的最小值．
(2)如图2，过点E作EF∥AP交x轴于点F，若以A、P、E、F为顶点的四边形是平行四边形，求直线PE的解析式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】把长为20，宽为a的长方形纸片(10＜a＜20)，如图那样折一下，剪下一个边长等于长方形宽度的正方形(称为第一次操作)；再把剩下的长方形如图那样折一下，剪下一个边长等于此时长方形宽度的正方形(称为第二次操作)；如此反复操作下去，若在第n次操作后，剩下的长方形为正方形，则操作停止．当n=3时，a的值为________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点O为Rt△ABC斜边AB上一点，以OA为半径的⊙O与BC相切于点D，与AC相交于点E，与AB相交于点F，连接AD．
（1）求证：AD平分∠BAC；
（2）若点E为弧AD的中点，探究线段BD，CD之间的数量关系，并证明你的结论；
（3）若点E为弧AD的中点，CD=
，求弧DF与线段BD，BF所围成的阴影部分的面积．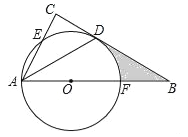
相关试题
