【题目】如图 1,是一个长为 2m,宽为 2n 的长方形,沿图中虚线用剪刀将其均分成四个完全相同的小长方形,然后按图 2 的形状拼图.
(1)图 2 中的图形阴影部分的边长为 ;(用含 m、n 的代数式表示)
(2)请你用两种不同的方法分别求图 2 中阴影部分的面积; 方法一: ;方法二: .
(3)观察图 2,请写出代数式(m+n)2、(m﹣n)2、4mn 之间的关系式: .

参考答案:
【答案】(1) m﹣n;(2)(m﹣n)2 ;(m+n)2﹣4mn ;(3) (m﹣n)2 =(m+n)2﹣4mn .
【解析】
(1)根据小长方形的长、宽分别为 m、n 即可得出答案;
(2)方法一:直接利用正方形面积=边长×边长;方法二:大正方形的面积减去大长方形的面积;
(3)根据方法二的表达式即可得出三者的关系式.
(1)阴影部分的边长=m﹣n;
(2)方法一:阴影部分的面积=(m﹣n)(m﹣n)=(m﹣n)2;
方法二:大正方形的面积=(m+n)2,大长方形的面积=4mn,
则阴影部分的面积=(m+n)2﹣4mn;
(3)由(2)可得:(m+n)2﹣4mn=(m﹣n)2;
故答案为:m﹣n;(m﹣n)2;(m+n)2﹣4mn;(m+n)2﹣4mn=(m﹣n)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )
A.
B.
C.
D.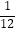
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线距离之和PE+PF是( )
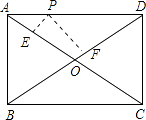
A.4.8
B.5
C.6
D.7.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的对角线AC,BD交于点O,点E,F分别是OB,OC上的动点.当动点E,F满足BE=CF时.
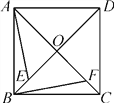
(1)写出所有以点E或F为顶点的全等三角形;(不得添加辅助线)
(2)求证:AE⊥BF.
-
科目: 来源: 题型:
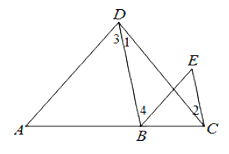
查看答案和解析>>【题目】按图填空,并注明理由.
已知: 如图,∠1=∠2,∠3=∠E. 求证:AD∥BE.
证明: ∵∠1=∠2 (已知)
∴ BD ∥ ( )
∴ ∠E = ( )
又 ∵ ∠E=∠3 ( 已知 )
∴ ∠3=∠ ( )
∴ AD∥BE.( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过(﹣2,0),则下列结论:①bc>0;②b+2a=0;③a+c>b;④16a+4b+c=0;⑤3a+c<0,其中正确结论的个数是( )
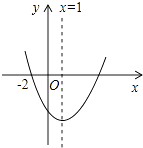
A.5
B.4
C.3
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,M是AC上一点,N是BC上一点,且AM=BN,∠MBC=25°,AN与BM交于点O,则∠MON的度数为( )
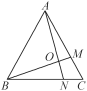
A. 110° B. 105° C. 90° D. 85°
相关试题

