【题目】如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )
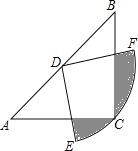
A. 由小到大 B. 由大到小 C. 不变 D. 先由小到大,后由大到小
参考答案:
【答案】C
【解析】试题分析:作DM⊥AC于M,DN⊥BC于N,构造正方形DMCN,利用正方形和等腰直角三角形的性质,通过证明△DMG≌△DNH,把△DHN补到△DNG的位置,得到四边形DGCH的面积=正方形DMCN的面积,于是得到阴影部分的面积=扇形的面积﹣正方形DMCN的面积,即为定值.
试题解析:解:作DM⊥AC于M,DN⊥BC于N,连接DC,
∵CA=CB,∠ACB=90°,
∴∠A=∠B=45°,
DM=![]() AD=
AD=![]() AB,DN=
AB,DN=![]() BD=
BD=![]() AB,
AB,
∴DM=DN,
∴四边形DNCN是正方形,
∴∠MDN=90°,
∴∠MDG=90°﹣∠GDN,
∵∠EDF=90°,
∴∠NDH=90°﹣∠GDN,
∴∠MDG=∠NDH,
在△DMG和△DNH中,
 ,
,
∴△DMG≌△DNH,
∴四边形DGCH的面积=正方形DMCN的面积,
∵正方形DMCN的面积=DM2=![]() AB2,
AB2,
∴四边形DGCH的面积=![]() ,
,
∵扇形FDE的面积=![]() =
=![]() ,
,
∴阴影部分的面积=扇形面积﹣四边形DGCH的面积=![]() (定值),
(定值),
故选C.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a+2a=3a2
B.a3a2=a5
C.(a4)2=a6
D.a4+a2=a4 -
科目: 来源: 题型:
查看答案和解析>>【题目】在3,4,﹣5,﹣6中,任取两个数相乘,积最大的是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )
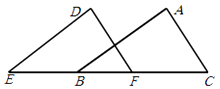
A.AB=DE
B.DF∥AC
C.∠E=∠ABC
D.AB∥DE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OP平分∠AOB,PC⊥OA,PD⊥OB,垂足分别是C、D.下列结论中错误的是( )。
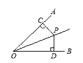
A.PC = PD
B.OC = OD
C.∠CPO = ∠DPO
D.OC = PC
相关试题

