【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
参考答案:
【答案】(1)y=﹣30x+2100.(2)每件售价定为55元时,每星期的销售利润最大,最大利润6750元.
(3)每星期至少要销售该款童装360件.
【解析】试题分析:(1)根据售量y(件)与售价x(元/件)之间的函数关系即可得到结论.
(2))设每星期利润为W元,构建二次函数利用二次函数性质解决问题.
(3)列出不等式先求出售价的范围,再确定销售数量即可解决问题.
试题解析:(1)y=300+30(60﹣x)=﹣30x+2100.
(2)设每星期利润为W元,
W=(x﹣40)(﹣30x+2100)=![]() .
.
∴x=55时,![]() =6750.
=6750.
∴每件售价定为55元时,每星期的销售利润最大,最大利润6750元.
(3)由题意(x﹣40)(﹣30x+2100)≥6480,解得52≤x≤58,
当x=52时,销售300+30×8=540,
当x=58时,销售300+30×2=360,
∴该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装360件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.x2x=2x
B.x3x2=x5
C.(x2)3=x5
D.(2x)2=2x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)16÷(﹣2)3﹣(﹣ )×(﹣4);
)×(﹣4);
(2)|﹣1 |×(0.5﹣
|×(0.5﹣  )÷1
)÷1  ;
;
(3)[1﹣(1﹣0.5× )]×[2﹣(﹣3)2]
)]×[2﹣(﹣3)2]
(4)﹣14﹣(1﹣0.5)× ×[10﹣(﹣2)2]﹣(﹣1)3 .
×[10﹣(﹣2)2]﹣(﹣1)3 . -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣1= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,错误的是( )
A.﹣62=﹣36
B.(﹣1)100+(﹣1)1000=0
C.(﹣4)3=﹣64
D.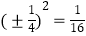
-
科目: 来源: 题型:
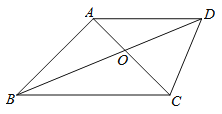
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,AB=AC=AD,∠DAC=∠ABC.
(1)求证:BD平分∠ABC;
(2)若∠DAC=45°,OA=1,求OC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从一个多边形的某个顶点出发,分别连接这个点和其余各顶点,可以把这个多边形分割成10个三角形,则这个多边形的边数为_____,过这个多边形的一个顶点能作___条对角线。
相关试题

