【题目】某中学对本校学生每天完成作业所用时间的情况进行抽样调查,随机调查了九年级部分学生每天完成作业所用的时间,并把统计结果制作成如图所示的频数分布直方图(时间取整数,图中从左至右依次为第一、二、三、四、五组)和扇形统计图.请结合图中信息解答下列问题.
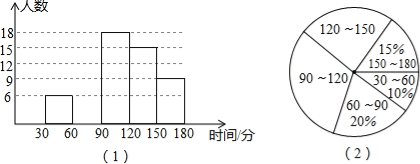
(1)本次调查的学生人数为 人;
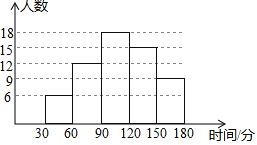
(2)补全频数分布直方图;
(3)根据图形提供的信息判断,下列结论正确的是 (只填所有正确结论的代号);
A.由图(1)知,学生完成作业所用时间的中位数在第三组内 |
B.由图(1)知,学生完成作业所用时间的众数在第三组内 |
C.图(2)中,90~120数据组所在扇形的圆心角为108° |
D.图(1)中,落在第五组内数据的频率为0.15 |
(4)学生每天完成作业时间不超过120分钟,视为课业负担适中.根据以上调查,估计该校九年级560名学生中,课业负担适中的学生约有多少人?
参考答案:
【答案】(1)60;(2)补全的频数分布直方图见解析;(3)ACD.(4)九年级学生中,课业负担适中的学生约为336人.
【解析】试题分析:(1)根据完成课外作业时间低于60分钟的学生数占被调查人数的10%.可求出抽查的学生人数;
(2)根据总人数,现有人数为补上那12人,画图即可;
(3)根据中位数、众数、频率的意义对各选项依次进行判断即可解答;
(4)先求出60人里学生每天完成课外作业时间在120分钟以下的人的比例,再按比例估算全校的人数.
试题解析:(1)6÷10%=60(人).
(2)补全的频数分布直方图如图所示:
(3)A.由图(1)知,学生完成作业所用时间的中位数在第三组内,正确;
B.由图(1)知,学生完成作业所用时间的众数不在第三组内,错误;
C.图(2)中,90~120数据组所在扇形的圆心角为108°.正确;
D.图(1)中,落在第五组内数据的频率为0.15,正确.
(4)![]() =60%,即样本中,完成作业时间不超过120分钟的学生占60%.
=60%,即样本中,完成作业时间不超过120分钟的学生占60%.
∴560×60%=336.
答:九年级学生中,课业负担适中的学生约为336人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8cm,BC=20cm,E是AD的中点.动点P从A点出发,沿A-B-C路线以1cm/秒的速度运动,运动的时间为t秒.将
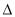 APE以EP为折痕折叠,点A的对应点记为M.
APE以EP为折痕折叠,点A的对应点记为M.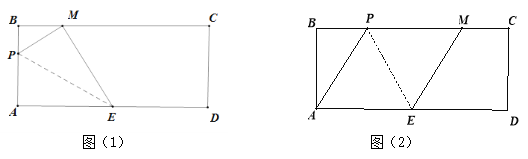
(1) 如图(1),当点P在边AB上,且点M在边BC上时,求运动时间t;
(2) 如图(2),当点P在边BC上,且点M也在边BC上时,求运动时间t;
(3) 直接写出点P在运动过程中线段BM长的最小值 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把a42a2b2+b4分解因式,结果是( )
A. a2(a22b2)+b4 B. (a2b2)2 C. (ab)4 D. (a+b)2(ab)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:①△A1AD1≌△CC1B;②s=
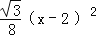 (0<x<2);③当x=1时,四边形ABC1D1是正方形;④当x=2时,△BDD1为等边三角形;其中正确的是 (填序号).
(0<x<2);③当x=1时,四边形ABC1D1是正方形;④当x=2时,△BDD1为等边三角形;其中正确的是 (填序号).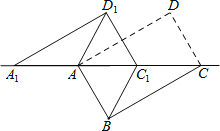
-
科目: 来源: 题型:
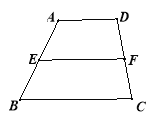
查看答案和解析>>【题目】(1)叙述三角形中位线定理,并运用平行四边形的知识证明;
(2)运用三角形中位线的知识解决如下问题:如图,在四边形ABCD中,AD∥BC,E,F分别是AB,CD的中点,求证EF=
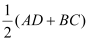 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)如图,直径为1的单位长度的圆,圆上的一点沿数轴向左滚动一周(不滑动)到达点A,则点A表示的数为_________;若此圆从表示1的点沿数轴滚动一周(不滑动)到达点C,写出点C所表示的数_______。(用含有
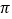 的式子表示)
的式子表示)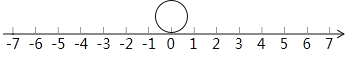
(2)通过观察,可以发现数轴上两点间距离与这两点表示数的差的绝对值有一定关系,如
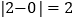 表示有理数2与0在数轴上所对应点之间的距离为2。按照此关系,数轴上表示x与-2的两点之间的距离可以表示为_________。
表示有理数2与0在数轴上所对应点之间的距离为2。按照此关系,数轴上表示x与-2的两点之间的距离可以表示为_________。(3)如果
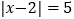 ,则x表示的有理数为__________。
,则x表示的有理数为__________。(4)同样道理,
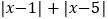 表示数轴上有理数x所对应的点到1和5所对应的点的距离之和。请你找出所有符合条件的整数x,使得
表示数轴上有理数x所对应的点到1和5所对应的点的距离之和。请你找出所有符合条件的整数x,使得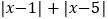 =4。
=4。 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列推理正确的是( )
A.弟弟今年13岁,哥哥比弟弟大6岁,到了明年,哥哥比弟弟只大5岁了,因为弟弟的明年比今年长大了1岁
B.如果a>b,b>c,则a>c
C.∠A与∠B相等,原因是它们看起来大小也差不多
D.因为对顶角必然相等,所以相等角也必是对顶角
相关试题

